题目内容
3.计算(1)-22+$\sqrt{4}$+(3-π)0-|-3|
(2)2a2-6a(a-b)+(a-3b)2
(3)($\frac{1}{x-1}$-1)÷$\frac{{x}^{2}+2x+1}{{x}^{2}-1}$
(4)$\frac{12}{{m}^{2}-9}$+$\frac{2}{m+3}$.
分析 (1)根据幂的乘方、零指数幂、绝对值可以解答本题;
(2)根据单项式乘多项式和完全平方公式可以解答本题;
(3)根据分式的减法和除法可以解答本题;
(4)根据分式的加法可以解答本题.
解答 解:(1)-22+$\sqrt{4}$+(3-π)0-|-3|
=-4+2+1-3
=-4;
(2)2a2-6a(a-b)+(a-3b)2
=2a2-6a2+6ab+a2-6ab+9b2
=-3a2+9b2;
(3)($\frac{1}{x-1}$-1)÷$\frac{{x}^{2}+2x+1}{{x}^{2}-1}$
=$\frac{1-x+1}{x-1}×\frac{(x+1)(x-1)}{(x+1)^{2}}$
=$\frac{2-x}{x-1}×\frac{(x+1)(x-1)}{(x+1)^{2}}$
=$\frac{(2-x)(x+1)}{(x+1)^{2}}$
=$\frac{-{x}^{2}+x+2}{{x}^{2}+2x+1}$;
(4)$\frac{12}{{m}^{2}-9}$+$\frac{2}{m+3}$
=$\frac{12}{(m+3)(m-3)}$+$\frac{2}{m+3}$
=$\frac{12+2(m-3)}{(m+3)(m-3)}$
=$\frac{2(m+3)}{(m+3)(m-3)}$
=$\frac{2}{m-3}$.
点评 本题考查分式的混合运算、单项式乘多项式、完全平方公式、零指数幂、绝对值,解答本题的关键是明确它们各自的计算方法.

练习册系列答案
相关题目
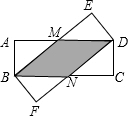 如图,已知四边形ABCD、四边形DEBF都是矩形,AB=BF,BE,AD交于点M,BC、DF交于点N,试说明四边形BMDN是菱形.
如图,已知四边形ABCD、四边形DEBF都是矩形,AB=BF,BE,AD交于点M,BC、DF交于点N,试说明四边形BMDN是菱形.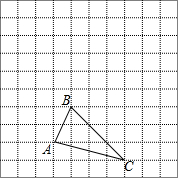 如图,已知单位长度为1的方格中有个△ABC,若A(-3,-3),B(-2,-1),C(0,-4).
如图,已知单位长度为1的方格中有个△ABC,若A(-3,-3),B(-2,-1),C(0,-4).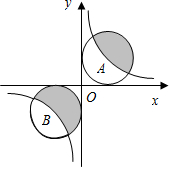 如图,⊙A和⊙B都与x轴和y轴相切,圆心A和圆心B都在反比例函数y=$\frac{3}{x}$的图象上,则图中阴影部分的面积等于3π.
如图,⊙A和⊙B都与x轴和y轴相切,圆心A和圆心B都在反比例函数y=$\frac{3}{x}$的图象上,则图中阴影部分的面积等于3π.