题目内容
已知直线y=-3x-3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称,经过点C的直线与y轴交于点D,与直线AB交于点E,且E点在第二象限.
(1)求A,B两点的坐标;
(2)若点D(0,1),如图2,过点B作BF⊥CD于F,连接BC,求∠DBF的度数及△BCE的面积;
(3)若点G(G不与C重合)是动直线CD上一点,且BG=BA,试探究∠ABG与∠ACE之间满足的等量关系,并加以证明.

(1)求A,B两点的坐标;
(2)若点D(0,1),如图2,过点B作BF⊥CD于F,连接BC,求∠DBF的度数及△BCE的面积;
(3)若点G(G不与C重合)是动直线CD上一点,且BG=BA,试探究∠ABG与∠ACE之间满足的等量关系,并加以证明.

考点:一次函数综合题
专题:代数综合题,分类讨论
分析:(1)利用图象与坐标轴相交是对应x,y的值进而得出A,B点坐标;
(2)根据点C的坐标求得OC=1.由D(0,1),得OD=1.求得直线CD的解析式为y=-x+1然后与直线y=3x-3联立即可求得两直线的交点E的坐标,过E作EH⊥y轴于H,则EH=2.再根据B、D的坐标求得BD=4.然后利用S△BCE=S△BDE+S△BDC即可求得三角形BCE的面积.
(3)连接BC,作BM⊥CD于M.设∠CBO=α,则∠ABO=α,∠ACB=90°-α,∠CBM=β,则∠GBM=β,∠BCG=90°-β.然后分当点G在射线CD的反向延长线上时和当点G在射线CD的延长线上时两种情况讨论即可得到答案.
(2)根据点C的坐标求得OC=1.由D(0,1),得OD=1.求得直线CD的解析式为y=-x+1然后与直线y=3x-3联立即可求得两直线的交点E的坐标,过E作EH⊥y轴于H,则EH=2.再根据B、D的坐标求得BD=4.然后利用S△BCE=S△BDE+S△BDC即可求得三角形BCE的面积.
(3)连接BC,作BM⊥CD于M.设∠CBO=α,则∠ABO=α,∠ACB=90°-α,∠CBM=β,则∠GBM=β,∠BCG=90°-β.然后分当点G在射线CD的反向延长线上时和当点G在射线CD的延长线上时两种情况讨论即可得到答案.
解答: 解:(1)∵直线y=-3x-3与x轴交于点A,与y轴交于点B,
解:(1)∵直线y=-3x-3与x轴交于点A,与y轴交于点B,
∴x=0时,y=-3,
y=0时,x=-1,
∴A(-1,0),B(0,-3);
(2)如解答中图1,依题意,C(1,0),OC=1.
由D(0,1),得OD=1.
在△DOC中,∠DOC=90°,OD=OC=1.
可得∠CDO=45°.
∵BF⊥CD于F,
∴∠BFD=90°.
∴∠DBF=90°-∠CDO=45°.
可求得直线CD的解析式为y=-x+1
由
,
解得
∴直线AB与CD的交点为E(-2,3).
过E作EH⊥y轴于H,则EH=2.
∵B(0,-3),D(0,1),
∴BD=4.
∴S△BCE=S△BDE+S△BDC=
×4×2+
×4×1=6;
(3)如解答中图2,连接BC,作BM⊥CD于M.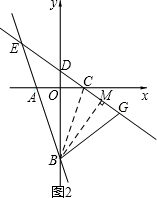
∵AO=OC,BO⊥AC,
∴BA=BC.
∴∠ABO=∠CBO.
设∠CBO=α,则∠ABO=α,∠ACB=90°-α.
∵BG=BA,
∴BG=BC.
∵BM⊥CD,
∴∠CBM=∠GBM.
设∠CBM=β,则∠GBM=β,∠BCG=90°-β.
(i) 如解答中图2,当点G在射线CD的反向延长线上时,
∵∠ABG=2α+2β=2(α+β)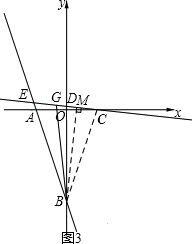
∠ECA=180°-(90°-α)-(90°-β)=α+β
∴∠ABG=2∠ECA.
(ii) 如解答中图3,当点G在射线CD的延长线上时,
∵∠ABG=2α-2β=2(α-β)
∠ECA=(90°-β)-(90°-α)=α-β
∴∠ABG=2∠ECA.
综上,∠ABG=2∠ECA.
 解:(1)∵直线y=-3x-3与x轴交于点A,与y轴交于点B,
解:(1)∵直线y=-3x-3与x轴交于点A,与y轴交于点B,∴x=0时,y=-3,
y=0时,x=-1,
∴A(-1,0),B(0,-3);
(2)如解答中图1,依题意,C(1,0),OC=1.
由D(0,1),得OD=1.
在△DOC中,∠DOC=90°,OD=OC=1.
可得∠CDO=45°.
∵BF⊥CD于F,
∴∠BFD=90°.
∴∠DBF=90°-∠CDO=45°.
可求得直线CD的解析式为y=-x+1
由
|
解得
|
∴直线AB与CD的交点为E(-2,3).
过E作EH⊥y轴于H,则EH=2.
∵B(0,-3),D(0,1),
∴BD=4.
∴S△BCE=S△BDE+S△BDC=
| 1 |
| 2 |
| 1 |
| 2 |
(3)如解答中图2,连接BC,作BM⊥CD于M.

∵AO=OC,BO⊥AC,
∴BA=BC.
∴∠ABO=∠CBO.
设∠CBO=α,则∠ABO=α,∠ACB=90°-α.
∵BG=BA,
∴BG=BC.
∵BM⊥CD,
∴∠CBM=∠GBM.
设∠CBM=β,则∠GBM=β,∠BCG=90°-β.
(i) 如解答中图2,当点G在射线CD的反向延长线上时,
∵∠ABG=2α+2β=2(α+β)

∠ECA=180°-(90°-α)-(90°-β)=α+β
∴∠ABG=2∠ECA.
(ii) 如解答中图3,当点G在射线CD的延长线上时,
∵∠ABG=2α-2β=2(α-β)
∠ECA=(90°-β)-(90°-α)=α-β
∴∠ABG=2∠ECA.
综上,∠ABG=2∠ECA.
点评:本题考查了一次函数的综合知识以及待定系数法求一次函数解析式等知识,题目中渗透了分类讨论的数学思想,题目难度较大.

练习册系列答案
相关题目
 如图,浦西对岸的高楼AB,在C处测得楼顶A的仰角为30°,向高楼前进100米到达D处,在D处测得A的仰角为45°,求高楼AB的高.
如图,浦西对岸的高楼AB,在C处测得楼顶A的仰角为30°,向高楼前进100米到达D处,在D处测得A的仰角为45°,求高楼AB的高. 如图,∠1=∠2,AB=AD,若使△ABC≌△ADE,则还需添加的一个条件是
如图,∠1=∠2,AB=AD,若使△ABC≌△ADE,则还需添加的一个条件是