题目内容
11.利用配方法求出关于x的一元二次方程的根,ax2+bx+c=0(a≠0),并指出其根的个数,若有两个根,两根的和与积.分析 方程整理后,利用完全平方公式变形,根据b2-4ac与0的关系判断其根的情况,进而求出两根的和与积.
解答 解:方程ax2+bx+c=0(a≠0),
变形得:x2+$\frac{b}{a}$x+$\frac{c}{a}$=0,即x2+$\frac{b}{a}$x=-$\frac{c}{a}$,
配方得:x2+$\frac{b}{a}$x+$\frac{{b}^{2}}{4{a}^{2}}$=$\frac{{b}^{2}-4ac}{4{a}^{2}}$,即(x+$\frac{b}{2a}$)2=$\frac{{b}^{2}-4ac}{4{a}^{2}}$,
当b2-4ac=0时,方程有两个相等的实数根为x1=x2=-$\frac{b}{2a}$;此时x1+x2=-$\frac{b}{a}$,x1x2=$\frac{{b}^{2}}{4{a}^{2}}$=$\frac{4ac}{4{a}^{2}}$=$\frac{c}{a}$;
当b2-4ac<0时,方程无解;
当b2-4ac>0时,方程有两个不相等的实数根,x1=$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$,x2=$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$,此时x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.
点评 此题考查了解一元二次方程-配方法,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
相关题目
20.下列二次根式中属于最简二次根式的是( )
| A. | $\sqrt{{m}^{2}+{n}^{2}}$ | B. | $\sqrt{9a}$ | C. | $\sqrt{\frac{a}{3}}$ | D. | $\sqrt{0.2}$ |
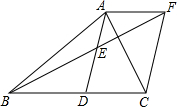 已知,如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交与BE的延长线于点F,且AF=DC,连结CF.
已知,如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交与BE的延长线于点F,且AF=DC,连结CF.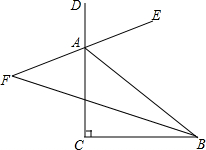 如图,在△ABC中,∠C=90°,∠ABC的平分线与外角∠BAD的平分线的反向延长线交于点F,则∠F=45°.
如图,在△ABC中,∠C=90°,∠ABC的平分线与外角∠BAD的平分线的反向延长线交于点F,则∠F=45°. 如图,ABCD是一块长方形场地,AB=42米,AD=25米,从A、B两处入口的小路都为1米,两小路汇合处路宽为2米,其余部分种植草坪,则草坪面积为960米2.
如图,ABCD是一块长方形场地,AB=42米,AD=25米,从A、B两处入口的小路都为1米,两小路汇合处路宽为2米,其余部分种植草坪,则草坪面积为960米2.