题目内容
1. 如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=$\frac{x}{y}$与正方形ABCD有公共点,则k的取值范围为( )
如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=$\frac{x}{y}$与正方形ABCD有公共点,则k的取值范围为( )| A. | 1<k<9 | B. | 2≤k≤34 | C. | 1≤k≤16 | D. | 4≤k<16 |
分析 根据题意求出点A的坐标,根据正方形的性质求出点C的坐标,根据反比例函数图象上点的坐标特征解答即可.
解答 解:∵点A在直线y=x上,横坐标为1,
∴点A的坐标为(1,1),
∵正方形ABCD的边长为3,
∴点C的坐标为(4,4),
当双曲线y=$\frac{x}{y}$经过点A时,k=1×1=1,
当双曲线y=$\frac{x}{y}$经过点C时,k=4×4=16,
∴双曲线y=$\frac{x}{y}$与正方形ABCD公共点,则k的取值范围是1≤k≤16,
故选C.
点评 本题考查的是反比例函数与一次函数的交点问题以及正方形的性质,掌握反比例函数图象上点的坐标特征、以及正方形的性质是解题的关键.

练习册系列答案
相关题目
11. 如图,△ABC≌△AED,AC与AD是对应边,AB与AE是对应边,则∠EAC等于( )
如图,△ABC≌△AED,AC与AD是对应边,AB与AE是对应边,则∠EAC等于( )
 如图,△ABC≌△AED,AC与AD是对应边,AB与AE是对应边,则∠EAC等于( )
如图,△ABC≌△AED,AC与AD是对应边,AB与AE是对应边,则∠EAC等于( )| A. | ∠ACB | B. | ∠BAC | C. | ∠BAD | D. | ∠CAD |
12.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. | 等边三角形 | B. | 平行四边形 | C. | 等腰三角形 | D. | 正六边形 |
6.下列计算正确的是( )
| A. | 2a+3b=6ab | B. | 19a2b2-9ab=10ab | C. | -2x2-2x2=0 | D. | 5y-3y=2y |
13.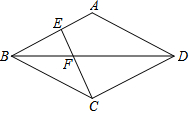 如图,菱形ABCD中,BD为ABCD的对角线,且CE⊥AB,交BD于点F,BD=8,AB=5,则CE的值是( )
如图,菱形ABCD中,BD为ABCD的对角线,且CE⊥AB,交BD于点F,BD=8,AB=5,则CE的值是( )
 如图,菱形ABCD中,BD为ABCD的对角线,且CE⊥AB,交BD于点F,BD=8,AB=5,则CE的值是( )
如图,菱形ABCD中,BD为ABCD的对角线,且CE⊥AB,交BD于点F,BD=8,AB=5,则CE的值是( )| A. | $\frac{12}{5}$ | B. | $\frac{24}{5}$ | C. | $\frac{48}{5}$ | D. | $\frac{8}{5}$ |