题目内容
△ABC∽△A′B′C′，AD，A′D′分别为△ABC和△A′B′C′的中线，若△ABC的周长为10，△A′B′C′的周长为12，则AD：A′D′= ．
考点：相似三角形的性质
专题：
分析：利用相似三角形的性质得出中线比以及周长比都等于相似比进而求出即可．
解答：解：∵△ABC∽△A′B′C′，AD，A′D′分别为△ABC和△A′B′C′的中线，△ABC的周长为10，△A′B′C′的周长为12，
∴两三角形的相似比为：5：6，
则AD：A′D′=5：6．
故答案为：5：6．
∴两三角形的相似比为：5：6，
则AD：A′D′=5：6．
故答案为：5：6．
点评：此题主要考查了相似三角形的性质，得出相似比是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，AD⊥BC，BE⊥AC，CF⊥AB，则△ABC中AC边上的高是（ ）| A、FC | B、BE | C、AD | D、AE |
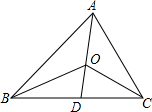已知△ABC，三个内角的角平分线交于点O，∠OCB=30°，求∠BOD．
如图，点A、O、B在一条直线上，∠1是锐角，则不是∠1的余角的是（ ）| A、∠2-90° | ||||
B、
| ||||
| C、90°-∠1 | ||||
D、
|