题目内容
19. 某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示).回答下列问题:
某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示).回答下列问题:(1)设这个苗圃园垂直于墙的一边的长为x米,则平行于墙的一边长为30-2x;(用含x的代数式表示)
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.
分析 (1)根据三边周长为30米即可得;
(2)由“平行于墙的一边长不小于8米、墙长为18米”可得x的范围,根据矩形的面积公式得出S关于x的函数解析式,配方成顶点式,利用二次函数的性质可得最值情况.
解答 解:(1)设这个苗圃园垂直于墙的一边的长为x米,则平行于墙的一边长为30-2x米,
故答案为:30-2x;
(2)根据题意得8≤30-2x≤18,
解得:6≤x≤11,
∵S=x(30-2x)=-2x2+30x=-2(x-$\frac{15}{2}$)2+$\frac{225}{2}$,
∴当x>$\frac{15}{2}$时,S随x的增大而减小,
∴当x=7.5时,S最大值=$\frac{225}{2}$;
当x=11时,S最小值=11×(30-22)=88.
点评 本题主要考查二次函数的应用,根据矩形的面积公式得出函数解析式是解题的根本,由题意求得x的范围,结合函数的性质求得最值是解题的关键.

练习册系列答案
相关题目
9.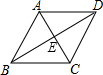 如图,要想证明平行四边形ABCD是菱形,下列条件中不能添加的是( )
如图,要想证明平行四边形ABCD是菱形,下列条件中不能添加的是( )
 如图,要想证明平行四边形ABCD是菱形,下列条件中不能添加的是( )
如图,要想证明平行四边形ABCD是菱形,下列条件中不能添加的是( )| A. | ∠ABD=∠ADB | B. | AC⊥BD | C. | AB=BC | D. | AC=BD |
9.某汽车销售店计划上半年每月销售20辆汽车,由于某种原因未能按计划执行,实际每月的销售情况如下表(规定比计划月销售量增加为正,减少为负):
(1)请把上表补充完整;
(2)销量最多的一个月比销量最少的一个月多销售多少辆?
(3)这半年内总销量比原计划多了还是少了?多或少了多少辆?
(4)这半年内实际平均每月销售了多少辆汽车?
| 月份 | 一 | 二 | 三 | 四 | 五 | 六 |
| 实际月销售(辆) | 24 | 19 | 22 | 23 | ||
| 比计划月销售量增(辆) | +4 | -2 | 0 | +3 |
(2)销量最多的一个月比销量最少的一个月多销售多少辆?
(3)这半年内总销量比原计划多了还是少了?多或少了多少辆?
(4)这半年内实际平均每月销售了多少辆汽车?
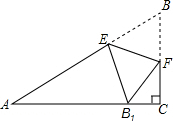 如图,在△ABC中,∠C=90°,点E,F分别在边AB,BC上,沿直线EF将△EBF翻折,使顶点B的对应点B1落在AC边上,且EB1⊥AC.求证:四边形BFB1E是菱形.
如图,在△ABC中,∠C=90°,点E,F分别在边AB,BC上,沿直线EF将△EBF翻折,使顶点B的对应点B1落在AC边上,且EB1⊥AC.求证:四边形BFB1E是菱形. 已知,如图,以矩形ABCD的一边CD为边向外作等边△PCD,请你用无刻度的直尺作出线段AB的垂直平分线(保留作图痕迹)
已知,如图,以矩形ABCD的一边CD为边向外作等边△PCD,请你用无刻度的直尺作出线段AB的垂直平分线(保留作图痕迹)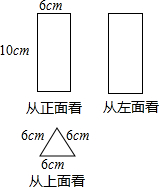 如图是从不同方向看一个几何体得到的形状图及部分数据:
如图是从不同方向看一个几何体得到的形状图及部分数据: