Question

11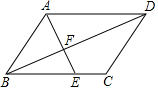．如图，在?ABCD中，E是BC上一点，AE交BD于F，BE=3，EC=2，S_△AFD=10，则S_△BEF=$\frac{18}{5}$．

Answer 1

分析 根据题目中的条件和所求问题，由三角形相似和相似三角形的面积比等于相似比的平方可以解答本题．

解答 解：∵在?ABCD中，E是BC上一点，AE交BD于F，BE=3，EC=2，
∴AD=BC，BC=BE+EC=5，AD∥BC，
∴△AFD∽△EFB，
∴$\frac{BE}{AD}=\frac{3}{5}$，
∴$\frac{{S}_{△BEF}}{{S}_{△DFA}}=（\frac{3}{5}）^{2}$，
∵S_△AFD=10，
∴S_△BEF=$\frac{18}{5}$，
故答案为：$\frac{18}{5}$．

点评 本题考查相似三角形的判定与性质、平行四边形的性质，解答本题的关键是明确题意，找出所求问题需要的条件，利用三角形的相似解答问题．