题目内容
6.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:| x | … | -3 | -2 | -1 | 0 | … |
| y | … | -2 | -5 | -6 | -5 | … |
分析 根据表格可求出该二次函数的对称轴为x=-1,然后求出(1,y)关于x=-1的对称点坐标,即可求出a+b+c的值.
解答 解:由表格可知:(-2,-5)与(0,-5)是关于对称轴对称的,
∴该二次函数的对称轴为x=-1,
设二次函数图象上的点为(1,y),(x,y)
由对称性可知:$\frac{1+x}{2}$=-1,
∴x=-3,
∴(1,y)与(-3,y)关于x=-1对称
由表格可知:x=-3时,y=-2,
令x=1代入y=ax2+bx+c,
∴y=a+b+c=-2
点评 本题考查二次函数图象上点的特征,解题的关键是求出该二次函数的对称轴,本题属于中等题型.

练习册系列答案
相关题目
20.下列调查中,适合用“普查”方式的是( )
| A. | 调查某型号节能灯泡的使用寿命 | |
| B. | 调查某品牌手机的市场占有率 | |
| C. | 调查我校初一(1)班的男女同学的比例 | |
| D. | 调查电视剧《芈月传》在全国的收视率 |
17.若∠P=25°12′,∠Q=25.12°,∠R=25.2°,则下列结论正确的是( )
| A. | ∠P=∠Q | B. | ∠P=∠R | C. | ∠Q=∠R | D. | ∠P=∠Q=∠R |
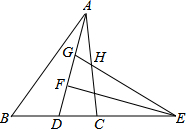 如图,在△ABC中,2AB=3AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H,若点H是AC的三等分点,则$\frac{AG}{GD}$为$\frac{2}{7}$或$\frac{4}{5}$..
如图,在△ABC中,2AB=3AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H,若点H是AC的三等分点,则$\frac{AG}{GD}$为$\frac{2}{7}$或$\frac{4}{5}$..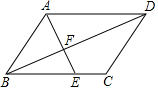 如图,在?ABCD中,E是BC上一点,AE交BD于F,BE=3,EC=2,S△AFD=10,则S△BEF=$\frac{18}{5}$.
如图,在?ABCD中,E是BC上一点,AE交BD于F,BE=3,EC=2,S△AFD=10,则S△BEF=$\frac{18}{5}$.