题目内容
4. 如图,在四边形ABCD中,∠B=90°,AB=BC=4,CD=6,DA=2.求四边形ABCD的面积.
如图,在四边形ABCD中,∠B=90°,AB=BC=4,CD=6,DA=2.求四边形ABCD的面积.
分析 利用勾股定理可求AC,求出AC2+DA2=CD2,由勾股定理的逆定理可证△ACD是直角三角形,由三角形的面积公式即可得出结果.
解答 解:如图所示,连接AC,
∵∠B=90°,AB=BC=4,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,
又∵CD=6,DA=2,
∴AC2+DA2=CD2,
∴△ACD是直角三角形,∠CAD=90°,
∴四边形ABCD的面积
=△ABC的面积+△ACD的面积
=$\frac{1}{2}$×4×4+$\frac{1}{2}$×2×4$\sqrt{2}$
=8+4$\sqrt{2}$.
点评 本题考查了等腰三角形的性质、勾股定理、勾股定理的逆定理.解题的关键是连接AC,并证明△ACD是直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14. 如图,△ABC中,点D在BC的延长线上,点F是AB边上一点,延长CA到E,连EF,则∠1,∠2,∠3的大小关系( )
如图,△ABC中,点D在BC的延长线上,点F是AB边上一点,延长CA到E,连EF,则∠1,∠2,∠3的大小关系( )
 如图,△ABC中,点D在BC的延长线上,点F是AB边上一点,延长CA到E,连EF,则∠1,∠2,∠3的大小关系( )
如图,△ABC中,点D在BC的延长线上,点F是AB边上一点,延长CA到E,连EF,则∠1,∠2,∠3的大小关系( )| A. | ∠1<∠2<∠3 | B. | ∠2<∠1<∠3 | C. | ∠3<∠2<∠1 | D. | ∠3<∠1<∠2 |
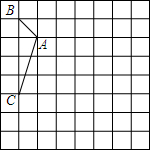 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求完成下列步骤:
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求完成下列步骤: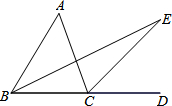 如图所示,∠ACD是△ABC的外角,∠A=40°,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.则∠E=20度.
如图所示,∠ACD是△ABC的外角,∠A=40°,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.则∠E=20度.