题目内容

14、函数y=x2+2x-8与x轴的交点坐标是
（2，0），（-4，0）
．
分析：解：令y=0，得方程x2+2x-8=0，根据十字相乘法求出方程的根，其就是函数与x轴交点的横坐标，从而求出函数y=x2+2x-8与x轴的交点坐标．
解答：解：令y=0，得
方程x2+2x-8=0，
解方程得，x=2或-4，
∴函数y=x2+2x-8与x轴的交点坐标是：（2，0），（-4，0）．
点评：此题主要考查一元二次方程与函数的关系，函数与x轴的交点的横坐标就是方程的根，两者互相转化，要充分运用这一点来解题．
练习册系列答案
相关题目
10、若把二次函数y=x2-2x-3化为y=（x-h）2+k的形式，其中h，k为常数，则h+k=
-3
．
29、已知二次函数y=x2-2x-3的图象与x轴交于A、B两点（A在B的左侧），与y轴交于点C，顶点为D．
（1）求点A、B、C、D的坐标，并在下面直角坐标系中画出该二次函数的大致图象；
（2）说出抛物线y=x2-2x-3可由抛物线y=x2如何平移得到？
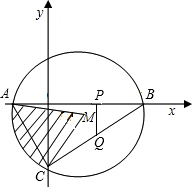精英家教网如图，已知二次函数y=x2-2x-3的图象与x轴交于点A、B两点，与y轴交于C点，⊙M是△ABC的外接圆．
（1）求阴影部分扇形AMC的面积；
（2）在x轴的正半轴上有一点P，作PQ⊥x轴交BC于Q，设PQ=K．
①设△OPQ的面积为S，求S关于K的函数关系式，并求出S的最大值；
②△CMQ能否与△AOC相似？若能，求出K的值；若不能，说明理由．
（2013•余姚市模拟）函数y=
k
x
和y=-
k
x
（k≠0）的图象关于y轴对称，我们把函数y=
k
x
和y=-
k
x
（k≠0）叫做互为“镜子”函数．类似地，如果函数y=f（x）和y=h（x）的图象关于y轴对称，那么我们就把函数y=f（x）和y=h（x）叫做互为“镜子”函数．
（1）请写出函数y=3x-4的“镜子”函数：
y=-3x-4
y=-3x-4
；
（2）函数
y=x2+2x+3
y=x2+2x+3
的“镜子”函数是y=x2-2x+3；
（3）如图，一条直线与一对“镜子”函数y=
2
x
（x＞0）和y=-
2
x
（x＜0）的图象分别交于点A、B、C，如果CB：AB=1：2，点C在函数y=-
2
x
（x＜0）的“镜子”函数上的对应点的横坐标是
1
2
，求点B的坐标．
定义符号yx表示与自变量x所对应的函数值．例如对于函数y=x2-2x+4，当x=2时，对应的函数值y=4，则可以写为：y2=4．在二次函数y=ax2+bx+c（a＞0）中，若yt+1=y-t+1对任意实数t都成立，那么下列结论错误的是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网