题目内容
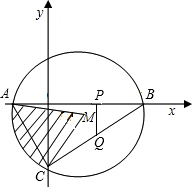 如图,已知二次函数y=x2-2x-3的图象与x轴交于点A、B两点,与y轴交于C点,⊙M是△ABC的外接圆.
如图,已知二次函数y=x2-2x-3的图象与x轴交于点A、B两点,与y轴交于C点,⊙M是△ABC的外接圆.(1)求阴影部分扇形AMC的面积;
(2)在x轴的正半轴上有一点P,作PQ⊥x轴交BC于Q,设PQ=K.
①设△OPQ的面积为S,求S关于K的函数关系式,并求出S的最大值;
②△CMQ能否与△AOC相似?若能,求出K的值;若不能,说明理由.
分析:(1)令y=0求出A点、B点的坐标,当x=0,求出C点的坐标,求出∠OBC=45°,求出∠M=90°,根据勾股定理求出AC=
=
和AM=
,根据扇形的面积公式求出即可;
(2)①由PQ⊥AB,∠PBQ=45°得出∠PBQ=∠PQB=45°,求出OP=OB-BP=3-k,根据三角形的面积公式s=
•OP•PQ即可求出答案;②当A、M、Q点在同一直线上时,由∠ACO=∠QCM,∠AOC=∠QMC=90°,得到△CMQ∽△AOC,根据勾股定理求出BQ=
=
k,BC=
=3
,推出CQ=3
-
k,代入
=
,即可求出k的值.
| OA2+OC2 |
| 10 |
| 5 |
(2)①由PQ⊥AB,∠PBQ=45°得出∠PBQ=∠PQB=45°,求出OP=OB-BP=3-k,根据三角形的面积公式s=
| 1 |
| 2 |
| BP2+PQ2 |
| 2 |
| OB2+OC2 |
| 2 |
| 2 |
| 2 |
| AC |
| CQ |
| CO |
| CM |
解答: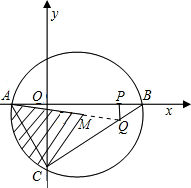 解:(1)令y=x2-2x-3=0,
解:(1)令y=x2-2x-3=0,
∴x1=3,x2=-1,
∴A点(-1,0),B点(3,0),
∴OB=3,OA=1,
令x=0,则y=-3,
∴C点(0,-3),
∴OC=3,
∴OB=OC,
∵∠BOC=90°,
∴∠OBC=45°,
∴∠M=90°,
在Rt△AOC中,AC=
=
,
在Rt△AMC中,AM2+MC2=AC2,AM=BM,
∴AM=
,
∴S扇形AMC=
=
,
答:阴影部分扇形AMC的面积是
.
(2)①∵PQ⊥AB,∠PBQ=45°,
∴∠PBQ=∠PQB=45°,
∴PB=PQ=K,
∴OP=OB-BP=3-k,
∴s=
•OP•PQ=
k(3-k)=-
k2+
k=-
(k-
)2+
,
∴s的最大值是
,
答:设△OPQ的面积为S,S关于k的函数关系式是s=-
k2+
k,S的最大值是
.
②当A、M、Q点在同一直线上时,
∠ACO=∠QCM,∠AOC=∠QMC=90°,
则△CMQ∽△AOC,
在Rt△BPQ中,根据勾股定理得BQ=
=
k,
在Rt△OBC中,根据勾股定理得:BC=
=3
,
∴CQ=3
-
k,
∴
=
,
∴
=
,
∴k=
,
答:△CMQ能与△AOC相似,此时k的值是
.
 解:(1)令y=x2-2x-3=0,
解:(1)令y=x2-2x-3=0,∴x1=3,x2=-1,
∴A点(-1,0),B点(3,0),
∴OB=3,OA=1,
令x=0,则y=-3,
∴C点(0,-3),
∴OC=3,
∴OB=OC,
∵∠BOC=90°,
∴∠OBC=45°,
∴∠M=90°,
在Rt△AOC中,AC=
| OA2+OC2 |
| 10 |
在Rt△AMC中,AM2+MC2=AC2,AM=BM,
∴AM=
| 5 |
∴S扇形AMC=
90×π(
| ||
| 360 |
| 5π |
| 4 |
答:阴影部分扇形AMC的面积是
| 5π |
| 4 |
(2)①∵PQ⊥AB,∠PBQ=45°,
∴∠PBQ=∠PQB=45°,
∴PB=PQ=K,
∴OP=OB-BP=3-k,
∴s=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 8 |
∴s的最大值是
| 9 |
| 8 |
答:设△OPQ的面积为S,S关于k的函数关系式是s=-
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 8 |
②当A、M、Q点在同一直线上时,
∠ACO=∠QCM,∠AOC=∠QMC=90°,
则△CMQ∽△AOC,
在Rt△BPQ中,根据勾股定理得BQ=
| BP2+PQ2 |
| 2 |
在Rt△OBC中,根据勾股定理得:BC=
| OB2+OC2 |
| 2 |
∴CQ=3
| 2 |
| 2 |
∴
| AC |
| CQ |
| CO |
| CM |
∴
| ||||
3
|
| 3 | ||
|
∴k=
| 4 |
| 3 |
答:△CMQ能与△AOC相似,此时k的值是
| 4 |
| 3 |
点评:本题主要考查对三角形的面积,勾股定理,三角形的外接圆与外心,圆周角定理,相似三角形的性质和判定,等腰三角形的性质和判定,勾股定理,解一元一次方程,扇形的面积,二次函数图象上点的坐标特征,二次函数的最值,三角形的内角和定理等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键,题型较好,综合性强.

练习册系列答案
相关题目
 三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.
三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.
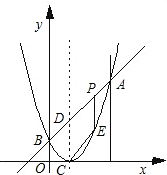 如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+b与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上.点P为线段AB上的一个动点(点P与A、B不重合),过点P作x轴的垂线与该二次函数的图象交于点E.
如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+b与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上.点P为线段AB上的一个动点(点P与A、B不重合),过点P作x轴的垂线与该二次函数的图象交于点E.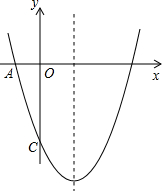 如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点C(0,-5).
如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点C(0,-5).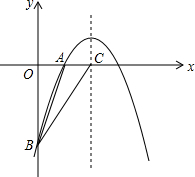 (2012•衡水一模)如图,已知二次函数
(2012•衡水一模)如图,已知二次函数