题目内容
11.已知一个正多边形的内角是108°,则过此多边形的一个顶点有2条对角线,可以把这个多边形分成3个三角形.分析 一个正多边形的每个内角都相等,根据内角与外角互为邻补角,因而就可以求出外角的度数.根据任何多边形的外角和都是360度,利用360除以外角的度数就可以求出外角和中外角的个数,即多边形的边数,进而得出过一个顶点可作对角线条数,以及分成的三角形个数.
解答 解:外角是:180°-108°=72(度),
360÷72=5,则这个多边形是正五边形,
过此多边形的一个顶点有2条对角线,可以把这个多边形分成3个三角形.
故答案为:2,3.
点评 此题考查了多边形内角与外角,根据外角和的大小与多边形的边数无关,由外角和求正多边形的边数,是常见的题目,需要熟练掌握.

练习册系列答案
相关题目
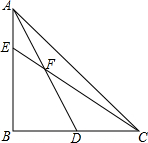 已知:△ABC中,AD是BC边中线,E是AB上一点,CE交直线AD于F,若CF=AB,求证:AE=EF.
已知:△ABC中,AD是BC边中线,E是AB上一点,CE交直线AD于F,若CF=AB,求证:AE=EF. 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G=540°.
如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G=540°.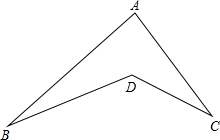 如图.点A、B、C、D是平面内四个点.连接AB、AC、BD、CD.
如图.点A、B、C、D是平面内四个点.连接AB、AC、BD、CD.