题目内容
15．
如图，五边形ABCDE的内角都相等，且∠1=∠2，∠3=∠4．求∠CAD的度数．
分析 由五边形ABCDE的内角都相等，先求出五边形的每个内角度数，再求出∠1=∠2=∠3=∠4=36°，从而求出∠CAD=108°-72°=36度．
解答 解：∵五边形的内角和是540°，
∴每个内角为540°÷5=108°，
∴∠E=∠B=∠BAE=108°，
又∵∠1=∠2，∠3=∠4，由三角形内角和定理可知，
∠1=∠2=∠3=∠4=（180°-108°）÷2=36°，
∴∠CAD=∠BAE-∠1-∠3=108°-36°-36°=36°．
点评 本题主要考查了正五边形的内角和以及正五边形的有关性质．解此题的关键是能够求出∠1=∠2=∠3=∠4=36°，和正五边形的每个内角是108度．
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
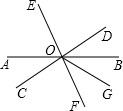如图所示，直线AB、CD、EF交于点O，OG平分∠BOF，且CD⊥EF，∠AOE=64°，求∠AOF、∠DOG的度数．
3．计算π0，结果是（ ）
| A． | 0 | B． | 1 | C． | π | D． | 3.14 |
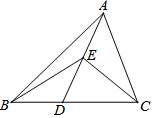如图，D是△ABC的边BC上的任意一点，E是AD的中点，若△ABC的面积为10，则△BCE的面积为5．
4．下列计算正确的是（ ）
| A． | 2÷$\frac{1}{2}$×2=2 | B． | $\frac{-n-m}{m+n}$=-1 | C． | a6÷a2=a3 | D． | （a+b）2=a2+b2 |