题目内容
5.解方程:(1)3x2-6x+1=0(用配方法);
(2)2x2-5x+2=0(公式法)
用适当的方法解下列方程:
(3)(2x-1)(x+3)=4.
(4)(2x-1)2-2(1-2x)=0.
分析 (1)根据配方法的一般步骤先把常数项移到等号的右边,再把二次项的系数化为1,再在等式两边同时加上一次项系数一半的平方,配成完全平方的形式,然后开方即可;
(2)找出a,b,c的值,代入求根公式即可求出值;
(3)先把要求的式子进行整理,然后进行因式分解,即可求出x的值;
(4)先把要求的式子进行变形,再提取公因式,即可求出x的值.
解答 解:(1)3x2-6x+1=0,
3x2-6x=-1,
x2-2x=-$\frac{1}{3}$,
x2-2x+1=$\frac{2}{3}$,
(x-1)2=$\frac{2}{3}$,
x-1=±$\frac{\sqrt{6}}{3}$,
x1=$\frac{\sqrt{6}}{3}$+1,x2=-$\frac{\sqrt{6}}{3}$+1;
(2)∵a=2,b=-5,c=2,
∴△=25-16=9,
∴x=$\frac{5±3}{4}$,
∴x1=2,x2=$\frac{1}{2}$;
(3)(2x-1)(x+3)=4,
2x2+5x-7=0,
(2x+7)(x-1)=0,
x1=-$\frac{7}{2}$,x2=1;
(4)(2x-1)2-2(1-2x)=0,
(2x-1)2+2(2x-1)=0,
(2x-1)(2x+1)=0,
x1=$\frac{1}{2}$,x2=-$\frac{1}{2}$.
点评 此题考查了一元二次方程的解法,解题时要注意解题步骤的准确应用.选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
13.下列各数中,是有理数是( )
| A. | $\frac{22}{7}$ | B. | π | C. | $\sqrt{2}$ | D. | $\sqrt{5}$ |
17.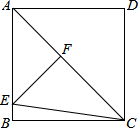 如图,在正方形ABCD中,AC为对角线,点E在AB边上,EF⊥AC于点F,连接EC,AF=3,△EFC的周长为12,则EC的长为( )
如图,在正方形ABCD中,AC为对角线,点E在AB边上,EF⊥AC于点F,连接EC,AF=3,△EFC的周长为12,则EC的长为( )
 如图,在正方形ABCD中,AC为对角线,点E在AB边上,EF⊥AC于点F,连接EC,AF=3,△EFC的周长为12,则EC的长为( )
如图,在正方形ABCD中,AC为对角线,点E在AB边上,EF⊥AC于点F,连接EC,AF=3,△EFC的周长为12,则EC的长为( )| A. | $\frac{7\sqrt{2}}{2}$ | B. | 3$\sqrt{2}$ | C. | 5 | D. | 6 |
14.下列运算结果是x+1的是( )
| A. | $\frac{{x}^{2}+1}{x+1}$ | B. | $\frac{1-{x}^{2}}{x+1}$ | C. | $\frac{x-1}{{x}^{2}-1}$ | D. | $\frac{{x}^{2}}{x-1}$$+\frac{1}{1-x}$ |
15.随着电子商务的发展,越来越多的人选择网上购物,导致各地商铺出租价格持续走低,某商业街的商铺今年1月份的出租价格为a元/平方米,2月份比1月份下降了5%,若3,4月份的出租价格按相同的百分率x继续下降,则4月份该商业街商铺的出租价格为:( )
| A. | (1-5%)a(1-2x)元 | B. | (1-5%)a(1-x)2元 | C. | (a-5%)(a-2)x元 | D. | a(1-5%-2x)元 |
 如图,五边形ABCDE的内角都相等,且∠1=∠2,∠3=∠4.求∠CAD的度数.
如图,五边形ABCDE的内角都相等,且∠1=∠2,∠3=∠4.求∠CAD的度数.