题目内容
5.若规定|a,b|表示a、b两个数中的最大值,则直线y=kx-1与函数y=|-x2,x-2|的图象有且只有一个交点,则k的范围是k<0或k>$\frac{3}{2}$.分析 画出函数图象,结合图象,首先求出直线y=x-2与抛物线y=-x2的交点A(1,-1),B(-2,-4)与直线y=kx-1与y轴交于C(0,-1),再求出直线AC,BC的斜率,进而求得k的范围.
解答 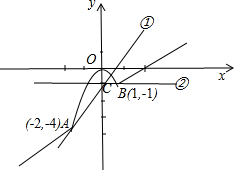 解:解方程组$\left\{\begin{array}{l}{y=-{x}^{2}}\\{y=x-2}\end{array}\right.$得:$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=-1}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-2}\\{{y}_{2}=-4}\end{array}\right.$,
解:解方程组$\left\{\begin{array}{l}{y=-{x}^{2}}\\{y=x-2}\end{array}\right.$得:$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=-1}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-2}\\{{y}_{2}=-4}\end{array}\right.$,
∴A(1,-1),B(-2,-4),
x=0时,y=kx-1=-1,
∴直线y=kx-1与y轴交于C(0,-1),
①kAC=$\frac{-1-(-4)}{0-(-2)}$=$\frac{3}{2}$(恰有两点,逆时针旋转至y轴时都满足),
∴k>$\frac{3}{2}$时,满足条件,
②kBC=0(恰有两点,逆时针旋转至y轴时都满足),
∴k<0时,满足条件,
综上:满足条件时,k≤0或k>$\frac{3}{2}$,
故答案为:k≤0或k>$\frac{3}{2}$.
点评 本题主要考查了求函数交点的方法,求直线斜率,掌握分类和数形结合的思想方法是解体的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
16.已知实数x,y,z满足x+y+z=5,xy+yz+zx=3,则z的最大值与最小值之和( )
| A. | $\frac{7}{3}$ | B. | $\frac{8}{3}$ | C. | $\frac{10}{3}$ | D. | $\frac{11}{3}$ |
10.关于?ABCD的叙述,正确的是( )
| A. | 若AC⊥BD,则?ABCD是正方形 | B. | 若AC=BD,则?ABCD是正方形 | ||
| C. | 若AB⊥BC,则?ABCD是菱形 | D. | 若AB=BC,则?ABCD是菱形 |
14.要使式子$\frac{\sqrt{x-1}}{2}$等于0,则x满足的条件是( )
| A. | x=1 | B. | x>-1 | C. | x≥1 | D. | x≥-1 |
 某景区的三个景点A,B,C在同一线路上,甲,乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C,甲,乙两人离开景点A后的路程S(米)关于时间t(分钟)的函数图象如图所示.根据信息回答下列问题:
某景区的三个景点A,B,C在同一线路上,甲,乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C,甲,乙两人离开景点A后的路程S(米)关于时间t(分钟)的函数图象如图所示.根据信息回答下列问题: 如图,已知∠AOE=∠COD,且射线OC平分∠BOE,∠EOD=30°,求∠AOD的度数.
如图,已知∠AOE=∠COD,且射线OC平分∠BOE,∠EOD=30°,求∠AOD的度数. 如图,五边形ABCDE的内角都相等,且∠1=∠2,∠3=∠4.求∠CAD的度数.
如图,五边形ABCDE的内角都相等,且∠1=∠2,∠3=∠4.求∠CAD的度数.