题目内容
5.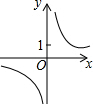 已知直线y=kx+1与双曲线y=$\frac{4}{x}$(如图所示).
已知直线y=kx+1与双曲线y=$\frac{4}{x}$(如图所示).(1)写出直线y=kx+1经过的定点坐标;
(2)对于k,试探索该直线与双曲线的交点情况.
分析 (1)由题意可知,直线y=kx+1经过的定点的横坐标一定是0,从而可以求得它的纵坐标,本题得以解决;
(2)先把两个解析式联立方程组,再看△的值,根据△的值,可以确定该直线与双曲线的交点情况,还要考虑k=0的情况.该直线与双曲线的交点情况.
解答 解:(1)当x=0时,不管k(k≠0)为何值,直线y=kx+1一定过点(0,1),
即直线y=kx+1经过的定点坐标是(0,1);
(2)$\left\{\begin{array}{l}{y=kx+1}\\{y=\frac{4}{x}}\end{array}\right.$
可得,kx2+x-4=0,
△=12-4×k×(-4)=1+16k,
当1+16k=0时,得k=-$\frac{1}{16}$,
∴当k>-$\frac{1}{16}$且k≠0时,该直线与双曲线有两个交点;
当k=-$\frac{1}{16}$时,该直线与双曲线有一个交点;
当k<-$\frac{1}{16}$时,该直线与双曲线没有交点;
∵当k=0时,y=1与x轴平行,此时该直线与双曲线有一个交点;
由上可得,当k>-$\frac{1}{16}$且k≠0时,该直线与双曲线有两个交点;
当k=-$\frac{1}{16}$或k=0时,该直线与双曲线有一个交点;
当k<-$\frac{1}{16}$时,该直线与双曲线没有交点.
点评 本题考查反比例函数与一次函数的交点问题,解题的关键是明确题意,找出所求问题需要的条件,注意要考虑k=0时的交点情况.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
13.如图,∠1和∠2是同位角的是( )
| A. |  | B. |  | C. |  | D. |  |
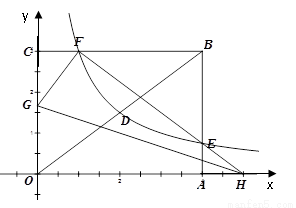
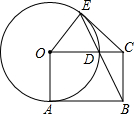 如图所示,在矩形OABC中,以O为圆心,OA为半径作圆,交OC,于点D,连接BD并延长,交⊙O于点E,连接OE,EC,EC=BC.
如图所示,在矩形OABC中,以O为圆心,OA为半径作圆,交OC,于点D,连接BD并延长,交⊙O于点E,连接OE,EC,EC=BC. 如图所示,直线AB与EF交于点O,已知∠AOD=∠COE=90°,写出图中与∠COD互余的角,这些角之间有什么关系?根据是什么?
如图所示,直线AB与EF交于点O,已知∠AOD=∠COE=90°,写出图中与∠COD互余的角,这些角之间有什么关系?根据是什么?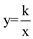 (k≠0)在第一象限内的图象经过点D、E,且
(k≠0)在第一象限内的图象经过点D、E,且
 B.
B.  C.
C.  D.
D.