题目内容
【题目】某校在开展“健康中国”读书征文评比活动中,对优秀征文予以评奖,并颁发奖品,奖品有甲、乙、丙三种类型.已知![]() 个丙种奖品的价格是
个丙种奖品的价格是![]() 个甲种奖品价格的
个甲种奖品价格的![]() 倍,
倍,![]() 个乙种奖品的价格比
个乙种奖品的价格比![]() 个甲种奖品的价格多
个甲种奖品的价格多![]() 元.用
元.用![]() 元分别去购买甲、乙、丙三种奖品,购买到甲和丙两种奖品的总数量是乙种奖品数量的
元分别去购买甲、乙、丙三种奖品,购买到甲和丙两种奖品的总数量是乙种奖品数量的![]() 倍.
倍.
(1)求![]() 个甲、乙、丙三种奖品的价格分别是多少元?
个甲、乙、丙三种奖品的价格分别是多少元?
(2)该校计划:购买甲、乙、丙三种奖品共![]() 个,其中购买甲种奖品的数量是丙种奖品的
个,其中购买甲种奖品的数量是丙种奖品的![]() 倍,且甲种奖品的数量不少于乙、丙两种奖品的数量之和.求该校完成购买计划最多要花费多少元?
倍,且甲种奖品的数量不少于乙、丙两种奖品的数量之和.求该校完成购买计划最多要花费多少元?
【答案】(1)![]() 个甲、乙、丙三种奖品的价格分别是
个甲、乙、丙三种奖品的价格分别是![]() 元、
元、![]() 元、
元、![]() 元;(2)该校完成购买计划最多要花费
元;(2)该校完成购买计划最多要花费![]() 元
元
【解析】
(1)设![]() 个甲种奖品的价格为
个甲种奖品的价格为![]() 元,则
元,则![]() 个丙种奖品的价格为
个丙种奖品的价格为![]() 元,
元,![]() 个乙种奖品的价格为
个乙种奖品的价格为![]() 元,根据“用
元,根据“用![]() 元分别去购买甲、乙、丙三种奖品,购买到甲和丙两种奖品的总数量是乙种奖品数量的
元分别去购买甲、乙、丙三种奖品,购买到甲和丙两种奖品的总数量是乙种奖品数量的![]() 倍”列方程并解答;
倍”列方程并解答;
(2)设购买丙种奖品![]() 个,则购买甲种奖品
个,则购买甲种奖品![]() 个,购买乙种奖品
个,购买乙种奖品![]() 个,根据“购买甲种奖品的数量不少于乙、丙两种奖品的数量之和”列不等式并解不等式,设该校购买奖品的费用为
个,根据“购买甲种奖品的数量不少于乙、丙两种奖品的数量之和”列不等式并解不等式,设该校购买奖品的费用为![]() 元,根据题意列出关系式:
元,根据题意列出关系式:![]() ,并根据这一次函数的性质即可求解.
,并根据这一次函数的性质即可求解.
解:(1)设![]() 个甲种奖品的价格为
个甲种奖品的价格为![]() 元,则
元,则![]() 个丙种奖品的价格为
个丙种奖品的价格为![]() 元,
元,![]() 个乙种奖品的价格为
个乙种奖品的价格为![]() 元,
元,
依题意,得:
![]()
解得:![]() ,
,
经检验,![]() 是原方程的解,且符合题意,
是原方程的解,且符合题意,
![]() ,
,![]() ,
,
故:![]() 个甲、乙、丙三种奖品的价格分别是
个甲、乙、丙三种奖品的价格分别是![]() 元、
元、![]() 元、
元、![]() 元;
元;
(2)设购买丙种奖品![]() 个,则购买甲种奖品
个,则购买甲种奖品![]() 个,购买乙种奖品
个,购买乙种奖品![]() 个,
个,
由题意有:![]() ,
,
![]() ,
,
设该校购买奖品的费用为![]() 元,则
元,则![]() ,
,
![]() 随
随![]() 的增大而减小,
的增大而减小,
![]() 时,
时,![]() 取最大值,且
取最大值,且![]() .
.
故:该校完成购买计划最多要花费![]() 元.
元.

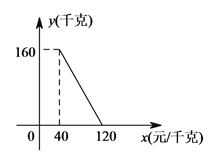
【题目】下面是十堰市的三个旅游景点:丹江口的武当山、房县的野人洞、郧西县的五龙河的部分门票价格表.某单位在国庆长假前期给每人购买了一张门票,现将购买门票的情况绘制成如图所示的柱状统计图.
景点 | 标价(元/张) |
武当山 | 200 |
野人洞 |
|
五龙河 | 80 |

请依据上表、图回答下列问题:
(1)去武当山旅游的门票有________张,购买去野人洞旅游的门票占所有门票张数的____________![]() .
.
(2)若该单位采取随机抽取的方式把门票分配给员工,在看不到门票的前提下,每人抽取一张(所有门票形状、大小、颜色等完全相同且充分洗匀).问员工小红抽取去武当山的门票的概率是___________.
(3)若购买去五龙河的总款数占全部款数的![]() .试求出每张野人洞门票的价格.
.试求出每张野人洞门票的价格.
【题目】已知函数y![]() ,请根据已学知识探究该函数的图象和性质.
,请根据已学知识探究该函数的图象和性质.
(1)列表,写出表中a、b,c的值:a= ,b= ,c= ;
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 0.5 | a | 2.5 | b | 2.5 | 1 | c | … |
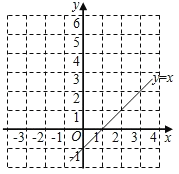
(2)描点,连线:在如图的平面直角坐标系中画出该函数的图象,并写出该函数的一条性质: ;
(3)已知函数y=x﹣1的图象如图所示,结合你所画的函数图象,直接写出不等式![]() x﹣1的解集: .
x﹣1的解集: .
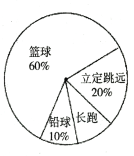
【题目】响应“阳光体育运动”号召,初三某班同学利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数(每人投10次)进行整理,作出如下统计图表.
进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
请你根据图表中的信息回答下列问题:
(1)训练后篮球定时定点投篮人均进球数为 个;进球数的中位数为 个,众数为 个;
(2)该班共有多少学生;
(3)根据测试资料,参加篮球定时定点投篮的学生训练后比训练前的人均进球增加了25%,求参加训练之前的人均进球数.