��Ŀ����
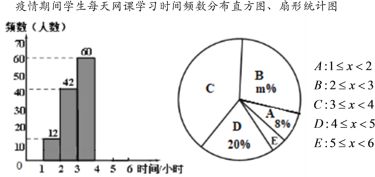
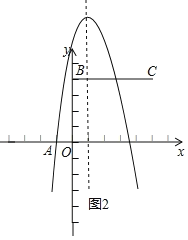
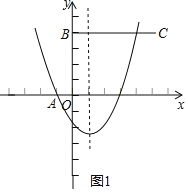
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y��mx��k����x�ᣬy��ֱ��ڵ�A��B��������A��������y��ax2��bx��3a��x����һ������Ϊ��D��AD��4������B����ƽ��5����λ���ȣ��õ���C��
��1�����C�����꣨��k��ʾ����
��2���������ߵĶԳ��
��3���������ߵĶԳ�����y���Ҳ࣬����BD��BD��BO��1�����������߶�BCǡ��һ�������㣬��ֱ��y��mx��k�Ľ���ʽ��a��ȡֵ��Χ��

���𰸡���1��C��5��k������2��x��1����x����1����3��y��4x��4��![]() ��
��![]() ��a����1��
��a����1��
��������
��1�������������ϵ���������������B�����꣬����ƽ�Ƶ����ʿ����C�����ꣻ
��2�������������ϵ���������������A�����꣬��һ����������ߵĶԳ��
��3�����ͼ�Σ��������������a��0����a��0���������ߵĶ������߶�BC�ϣ��������ۼ�����⣮
�⣺��1����y�ύ�㣺��x��0����ֱ��y��mx��k��y��k��
��B��0��k����
����B����ƽ��5����λ���ȣ��õ���C��
��C��5��k����
��2����y��0����������y��ax2��bx��3a�õ�x��![]()
��A��![]() ��0����D��
��0����D��![]() ��0��
��0��
��AD��4
��![]() ��4
��4
����ƽ���õ�
b2��4a(��3a)��16a2
��� b����2a��b��2a
�������ߵĶԳ���x��1����x����1��
��3���������ߵĶԳ�����y���Ҳ�
��x����![]() ��1 ��
��1 ��
��������y��ax2��2ax��3a
����A����1��0����D��3��0����
��BO��k����BD��k��1
��(k��1)2��k2��32
��k��4
��ֱ��y��mx��k����x�ᣬy��ֱ��ڵ�A��B
��ֱ��y��4x��4��
��a��0ʱ����ͼ1����x��0���������ߵ�y����3a��
�����������߶�BCǡ��һ�������㣬
����3a��4��a����![]() ��
��
��x��5���������ߵ�y��12a��
��12a��4��a��![]() ��
��
��a��![]() ��
��
��a��0ʱ����ͼ2����x��0���������ߵ�y����3a��
�����������߶�BCǡ��һ�������㣬
����3a��4��a����![]() ��
��
��x��5���������ߵ�y��12a��
��12a��4��a��![]() ��
��
��a����![]() ��
��
���������ߵĶ������߶�BC��ʱ����Ϊ��1��4����
��ͼ3�����㣨1��4�����������ߵ�4��a��2a��3a��
���a����1��
����������ֱ�ߵĽ���ʽΪy��4x��4��a��ȡֵ��ΧΪa��![]() ��a����
��a����![]() ��a����1��
��a����1��
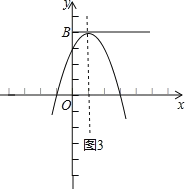

����Ŀ��ijУΪ���ѧ���忼�ɼ�����ȫУ300�����꼶ѧ������һ��������ѵ����Ϊ�˽�ѧ��ѵ��Ч����ѧУ�������ھ��꼶��ѧ�ڿ�ѧ����ѧ��ĩ�ֱ�Ծ��꼶ѧ������һ�����������ԣ�ѧ���ɼ���Ϊ����������20�֣�����18��Ϊ���㣮�������ȡ��ͬһ����ѧ�������γɼ����������������ͷ��������ɼ��÷���x��ʾ�����ֳ����飺A��x��13��B.13��x��15��C.15��x��17��D.17��x��19��E.19��x��20��
��ѧ����ȡѧ���ijɼ���D���е������ǣ�17��17��17��17��17��18��18��
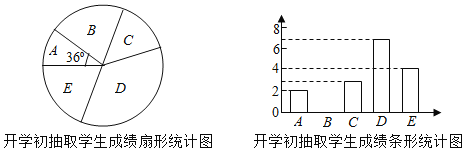
ѧ��ĩ��ȡѧ���ɼ�ͳ�Ʊ�
ѧ���ɼ� | A�� | B�� | C�� | D�� | E�� |
���� | 0 | 1 | 4 | 5 | a |
�������ݣ�
ƽ���� | ��λ�� | ���� | |
��ѧ����ȡѧ���ɼ� | 16 | b | 17 |
ѧ��ĩ��ȡѧ���ɼ� | 18 | 18.5 | 19 |
����������Ϣ������������⣺
��1��ֱ��д��ͼ����a��b��ֵ������ȫ����ͳ��ͼ��
��2�������У���꼶ѧ�����μ������β��ԣ����Ƹ�Уѧ��ĩ�ɼ������ѧ�������ȿ�ѧ���ɼ������ѧ�����������˶��٣�
��3��С��ѧ�����Գɼ�16�֣�ѧ��ĩ���Գɼ�19�֣����ݳ���������ݣ���ѡ��һ�����ʵ�ͳ��������С���ѵ��Ч����