题目内容
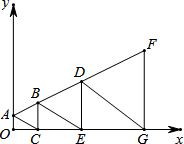 如图,在平面直角坐标系中,点A和点C分别在y轴和x轴的正半轴上,OA=a,∠ACO=30°,以线段AC为边在第一象限作等边三角形ABC,过点B作BE∥AC交x轴于点E,再以BE为边作第二个等边三角形BDE,…,依此方法作下去,则第n个等边三角形的面积是
如图,在平面直角坐标系中,点A和点C分别在y轴和x轴的正半轴上,OA=a,∠ACO=30°,以线段AC为边在第一象限作等边三角形ABC,过点B作BE∥AC交x轴于点E,再以BE为边作第二个等边三角形BDE,…,依此方法作下去,则第n个等边三角形的面积是考点:一次函数图象上点的坐标特征,等边三角形的性质
专题:规律型
分析:先根据OA=a,∠ACO=30°求出AC的长,再由△ABC是等边三角形可知BC⊥OG,由BE∥AC可知∠BEC=30°,故BE=2BC=4a,同理可得出△DGF的边长,再求出各三角形的面积,找出规律即可.
解答:解:∵OA=a,∠ACO=30°,
∴AC=2a.
∵△ABC是等边三角形,
∴BC⊥OG.
∵BE∥AC,
∴∠BEC=30°,
∴BE=2BC=4a,
同理可得,△DGF的边长=8a,…,
第n个等边三角形的边长=2na,
∴第n个等边三角形的面积=
•2na•2na•sin60°=
•22n.
故答案为:
•22n.
∴AC=2a.
∵△ABC是等边三角形,
∴BC⊥OG.
∵BE∥AC,
∴∠BEC=30°,
∴BE=2BC=4a,
同理可得,△DGF的边长=8a,…,
第n个等边三角形的边长=2na,
∴第n个等边三角形的面积=
| 1 |
| 2 |
| ||
| 4 |
故答案为:
| ||
| 4 |
点评:本题考查的是等边三角形的性质,根据直角三角形的性质求出等边三角形的边长是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列各式中,能用平方差公式分解因式的是( )
| A、x2+y2 |
| B、x2-y2 |
| C、-x2-y2 |
| D、x-y2 |
 如图是一个正方体的表面展开图,则元正方体中与“建”字所在的面相对面上标的字是(
如图是一个正方体的表面展开图,则元正方体中与“建”字所在的面相对面上标的字是(| A、美 | B、丽 | C、汉 | D、川 |
设a为
-
的小数部分,b为
-
的小数部分.则
-
的值为( )
3+
|
3-
|
6+3
|
6-3
|
| 2 |
| b |
| 1 |
| a |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,每个小正方形的边长都是1,△ABC的三个顶点分别在正方形网格的格点上,试判断△ABC的形状,并说明理由.
如图,每个小正方形的边长都是1,△ABC的三个顶点分别在正方形网格的格点上,试判断△ABC的形状,并说明理由.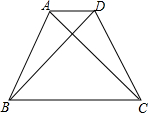 如图,等腰梯形ABCD的面积为144,AD∥BC,AB=DC,且AC⊥BD.求等腰梯形ABCD的高.
如图,等腰梯形ABCD的面积为144,AD∥BC,AB=DC,且AC⊥BD.求等腰梯形ABCD的高.