题目内容
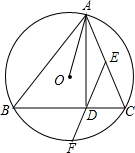
8.对于函数y=$\frac{2}{{x}^{2}+1}$可以分解为两个熟悉的函数:二次函数t=x2+1和反比例函数y=$\frac{2}{t}$,则函数y=$\frac{2}{{x}^{2}+1}$的取值范围是0<y≤2.分析 根据二次函数的性质确定t的最小值,再根据反比例函数的性质确定函数的取值范围.
解答 解:二次函数t=x2+1的性质:开口向上,顶点坐标(0,1),
所以当x=0时,函数有最小值1,即t≥1,
所以反比例函数y=$\frac{2}{t}$的图象在第一象限内,y随x的增大而减小,
当t=1时,y=2,
所以0<y≤2
故答案为:0<y≤2.
点评 本题考查的是二次函数和反比例函数的性质,确定二次函数t的最小值是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.如下表,方程1、方程2、方程3…是按照一定的规律排列的一列方程,解方程3,并将它的解填在表中的空白处.
(1)请写出这列方程中第m个方程,并写出它的解.
(2)用你探究的规律解方程x2-8x-20=0.
| 序号 | 方程 | 方程的解 | |
| 1 | x2+2x-3=0 | x1=1 | x2=-3 |
| 2 | x2+4x-12=0 | x1=2 | x2=-6 |
| 3 | x2+6x-27=0 | x1=3 | x2=-9 |
| … | … | … | … |
(2)用你探究的规律解方程x2-8x-20=0.
17.参加足球联赛的每两队之间都进行两场比赛,共要比赛90场,设共有x个队参加比赛,则下列方程符合题意的是( )
| A. | $\frac{1}{2}$x(x+1)=90 | B. | x(x+1)=90 | C. | $\frac{1}{2}$x(x-1)=90 | D. | x(x-1)=90 |
18.如图1,A,B,C是郑州市二七区三个垃圾存放点,点B,C分别位于点A的正北和正东方向,AC=40米.八位环卫工人分别测得的BC长度如下表:
他们又调查了各点的垃圾量,并绘制了下列尚不完整的统计图2,图3:
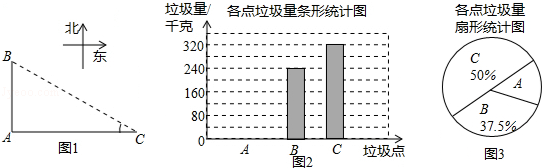
(1)求表中BC长度的平均数$\overline{x}$、中位数、众数;
(2)求A处的垃圾量,并将图2补充完整;
(3)用(1)中的$\overline{x}$作为BC的长度,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用.(注:$\sqrt{3}$=1.732)
| 甲 | 乙 | 丙 | 丁 | 戊 | 戌 | 申 | 辰 | |
| BC(单位:米) | 84 | 76 | 78 | 82 | 70 | 84 | 86 | 80 |

(1)求表中BC长度的平均数$\overline{x}$、中位数、众数;
(2)求A处的垃圾量,并将图2补充完整;
(3)用(1)中的$\overline{x}$作为BC的长度,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用.(注:$\sqrt{3}$=1.732)
 如图,已知△ABC内接于⊙O,AD⊥BC于D,E为AC的中点,延长ED交⊙O于F.
如图,已知△ABC内接于⊙O,AD⊥BC于D,E为AC的中点,延长ED交⊙O于F.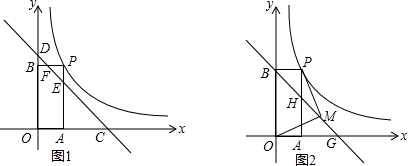
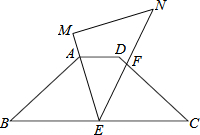 如图,等腰梯形ABCD中,AD∥BC,AD=$\sqrt{2}$,BC=4$\sqrt{2}$,∠B=45°,等腰直角三角板MEN的锐角顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.若△ABE为等腰三角形,则CF的长等于$\frac{5}{2}$或4$\sqrt{2}$-3或2.
如图,等腰梯形ABCD中,AD∥BC,AD=$\sqrt{2}$,BC=4$\sqrt{2}$,∠B=45°,等腰直角三角板MEN的锐角顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.若△ABE为等腰三角形,则CF的长等于$\frac{5}{2}$或4$\sqrt{2}$-3或2.