题目内容
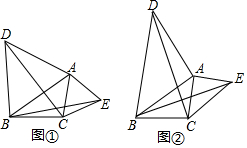
17.在菱形ABCD中,∠BAD=120°,△AEF等边三角形,且点C在边EF上,AE,AF分别交DC于点G,H.(1)如图1,连接AC,求证:①CG=DH;②△GCE∽△CAF.
(2)如图2,连接BD,交AE,AF于点O,P,若∠BAG=45°,DP=3,OP=4,求AB的长.

分析 (1)①根据菱形的想知道的∠B=∠BAC=∠CAD=60°,推出△ABC与△ACD是等边三角形,根据等边三角形的性质得到AC=AD,∠ACB=∠D=60°,得到∠GAC=∠DAH,根据全等三角形的性质得到CG=DH;②根据相似三角形的判定和性质即可得到结论;
(2)根据已知条件得到∠DAO=75°,由菱形的性质得到∠ADO=$\frac{1}{2}∠$ADC=30°,根据等腰三角形的性质即可得到结论.
解答 解:(1)①∵四边形ABCD是菱形,∠BAD=120°,
∴∠B=∠BAC=∠CAD=60°,
∴△ABC与△ACD是等边三角形,
∴AC=AD,∠ACB=∠D=60°,
∵△AEF是等边三角形,
∴∠EAF=60°,
∴∠GAC=∠DAH,
在△ACG与△ADH中,$\left\{\begin{array}{l}{∠GAC=∠HAD}\\{AC=AD}\\{∠ACG=∠D}\end{array}\right.$,
∴△ACG≌△ADH,
∴CG=DH;
②∵∠E=∠F=60°,
∵∠CGE=∠ACG+∠GAC=60°+∠GAC,
∠ACF=∠E+∠GAC=60°+∠GAC,
∴△GCE∽△CAF;
(2)∵∠BAG=45°,∠BAD=120°,
∴∠DAO=75°,
∵∠ADO=$\frac{1}{2}∠$ADC=30°,
∴∠AOD=75°,
∴∠DAO=∠AOD,
∴AD=OD=OP+DP=7,
∴AB=7.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定和性质,菱形的性质,等边三角形的性质,等腰三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
12.下列图形中,既是轴对称图形又是中心对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.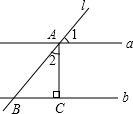 如图,直线a∥b,直线l与a,b分别交于点A,B,过点A作AC⊥b于点C,若∠1=50°,则∠2的度数为( )
如图,直线a∥b,直线l与a,b分别交于点A,B,过点A作AC⊥b于点C,若∠1=50°,则∠2的度数为( )
 如图,直线a∥b,直线l与a,b分别交于点A,B,过点A作AC⊥b于点C,若∠1=50°,则∠2的度数为( )
如图,直线a∥b,直线l与a,b分别交于点A,B,过点A作AC⊥b于点C,若∠1=50°,则∠2的度数为( )| A. | 130° | B. | 50° | C. | 40° | D. | 25° |
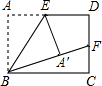 如图,在矩形ABCD中,E、F分别是AD、CD的中点,沿着BE将△ABE折叠,点A刚好落在BF上,若AB=2,则AD=2$\sqrt{2}$.
如图,在矩形ABCD中,E、F分别是AD、CD的中点,沿着BE将△ABE折叠,点A刚好落在BF上,若AB=2,则AD=2$\sqrt{2}$. 甲、乙两人在一段笔直的公路AB上行走,甲从A地出发前往B地,乙从B地出发前往A地,已知A、B两地相距4千米,乙比甲晚出发20分钟,甲、乙两人离A地的距离y(千米)与甲出发后经过的时间x(分钟)之间的函数关系如图所示.
甲、乙两人在一段笔直的公路AB上行走,甲从A地出发前往B地,乙从B地出发前往A地,已知A、B两地相距4千米,乙比甲晚出发20分钟,甲、乙两人离A地的距离y(千米)与甲出发后经过的时间x(分钟)之间的函数关系如图所示.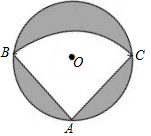 有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC.
有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC.