题目内容
 如图,在△ABC中,∠C=90°,D,E是BC边上的两点,且∠ABC=
如图,在△ABC中,∠C=90°,D,E是BC边上的两点,且∠ABC=| 1 |
| 2 |
| 1 |
| 3 |
考点:相似三角形的判定与性质,勾股定理
专题:计算题
分析:分析角的关系可知△ADE∽△BAE,得
=
=
.然后设EC=x,AC=y,根据勾股定理列方程,由AB2=BC2+AC2得(
)2=(16+x)2+y2,求得x、y即可.
| AD |
| BA |
| AE |
| BE |
| DE |
| AE |
44
| ||
| 5 |
解答:解:∵∠ABC=
∠ADC=
∠AEC,∴∠ABC=∠DAE,
又∵∠AEB=∠DEA(公共角),∴△ADE∽△BAE,则
=
=
.
由∠ABD=∠BAD,得AD=BD=11,BE=BD+DE=16.
∴AE2=BE•DE=16×5=80,AE=4
,AB=
=
.
设EC=x,AC=y,由AB2=BC2+AC2得(
)2=(16+x)2+y2,
即
=162+32x+x2+y2,但x2+y2=AE2=80,
于是
=256+32x+80,
x=
=1.6,y2=80-(
) 2=77.44,
y=8.8.
| 1 |
| 2 |
| 1 |
| 3 |
又∵∠AEB=∠DEA(公共角),∴△ADE∽△BAE,则
| AD |
| BA |
| AE |
| BE |
| DE |
| AE |
由∠ABD=∠BAD,得AD=BD=11,BE=BD+DE=16.
∴AE2=BE•DE=16×5=80,AE=4
| 5 |
| AD•AE |
| DE |
44
| ||
| 5 |
设EC=x,AC=y,由AB2=BC2+AC2得(
44
| ||
| 5 |
即
| 442 |
| 5 |
于是
| 442 |
| 5 |
x=
| 8 |
| 5 |
| 8 |
| 5 |
y=8.8.
点评:此题主要考查学生对相似三角形的判定与性质和勾股定理的理解和掌握,解答此题的关键是分析角的关系求证△ADE∽△BAE,得出
=
=
.此题难度较大,属于难题.
| AD |
| BA |
| AE |
| BE |
| DE |
| AE |

练习册系列答案
相关题目
要将40kg浓度为16%的盐水变为浓度为20%的盐水,则需蒸发掉水( )
| A、8kg | B、7kg |
| C、6kg | D、5kg |
 已知△ABC中,O为外心,I为内心,且AB+AC=2BC.求证:OI⊥AI(图).
已知△ABC中,O为外心,I为内心,且AB+AC=2BC.求证:OI⊥AI(图).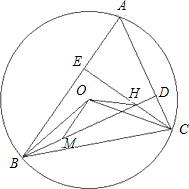 如图,⊙O为△ABC的外接圆,∠BAC=60°,H为边AC,AB上的高BD,CE的交点,在BD上取点M,使BM=CH.
如图,⊙O为△ABC的外接圆,∠BAC=60°,H为边AC,AB上的高BD,CE的交点,在BD上取点M,使BM=CH.