题目内容
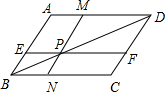 如图,?ABCD中,EF∥AD,MN∥AB,MN与EF交于点P,且点P在BD上.
如图,?ABCD中,EF∥AD,MN∥AB,MN与EF交于点P,且点P在BD上.(1)图中除了?ABCD外,还有
(2)图中面积相等的平行四边形有哪些?你能说明其中的原因吗?
考点:平行四边形的判定与性质
专题:
分析:(1)由平行和平行四这形的性质,可证明四边形ABNM、CDMN、ADFE、BCFE、AEPM、BEPN、DFPM、CFPN也为平行四边形;
(2)由平行四边形的性质可证明△ABD≌△CDB、△BEP≌△PNB、△PMD≌△DFP,再利用面积的和差可得出四边形AEPM和四边形CFPN面积相等,进一步可得到四边形ABNM和BCFE,四边形ADFE和CDMN的面积也相等.
(2)由平行四边形的性质可证明△ABD≌△CDB、△BEP≌△PNB、△PMD≌△DFP,再利用面积的和差可得出四边形AEPM和四边形CFPN面积相等,进一步可得到四边形ABNM和BCFE,四边形ADFE和CDMN的面积也相等.
解答:解:
(1)∵四边形ABCD为平行四边形,
∴AB∥CD,
又MN∥AB,
∴MN∥CD,
同理EF∥BC,
∴四边ABNM、CDMN、ADFE、BCFE、AEPM、BEPN、DFPM、CFPN为平行四边形,
故答案为:8.
(2)∵四边形ABCD为平行四边形,
∴AB=CD,AD=BC,
在△ABD和△CDB中
∴△ABD≌△CDB(SSS),
∴S△ABD=S△CDB,
同理可得S△BEP=S△PNB,S△PMD=S△DFP,
∴S△ABD-S△BEP-S△PMD=S△CDB-S△PNB-S△DFP,
∴S四边形AEPM=S四边形CFPN,
则S四边形ABNM=S四边形BCFE,S四边形ADFE=S四边形CDMN.
(1)∵四边形ABCD为平行四边形,
∴AB∥CD,
又MN∥AB,
∴MN∥CD,
同理EF∥BC,
∴四边ABNM、CDMN、ADFE、BCFE、AEPM、BEPN、DFPM、CFPN为平行四边形,
故答案为:8.
(2)∵四边形ABCD为平行四边形,
∴AB=CD,AD=BC,
在△ABD和△CDB中
|
∴△ABD≌△CDB(SSS),
∴S△ABD=S△CDB,
同理可得S△BEP=S△PNB,S△PMD=S△DFP,
∴S△ABD-S△BEP-S△PMD=S△CDB-S△PNB-S△DFP,
∴S四边形AEPM=S四边形CFPN,
则S四边形ABNM=S四边形BCFE,S四边形ADFE=S四边形CDMN.
点评:本题主要考查平行四边形的判定和性质,掌握平行四边形的判定和性质是解题的关键,即①两组对边分别平行的四边形?平行四边形,②两组对边分别相等的四边形?平行四边形,③一组对边分别平行且相等的四边形?平行四边形,④两组对角分别相等的四边形?平行四边形,⑤对角线互相平分的四边形?平行四边形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,△BCD的各个顶点都在⊙A上,△BCD的角平分线BF交CD于点E,交⊙A于点F,连结CF,求证:BE2=BC•BD-EC•ED.
如图,△BCD的各个顶点都在⊙A上,△BCD的角平分线BF交CD于点E,交⊙A于点F,连结CF,求证:BE2=BC•BD-EC•ED.

 如图,已知A(-3,-1)B(2,-1),在平面内画出一个以AB为一边的正方形,并写出这个正方形另外两个顶点的坐标.
如图,已知A(-3,-1)B(2,-1),在平面内画出一个以AB为一边的正方形,并写出这个正方形另外两个顶点的坐标. 利用网格作图(要求所画的三角形的顶点必须在格点上)
利用网格作图(要求所画的三角形的顶点必须在格点上)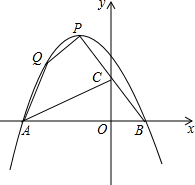 已知抛物线y=ax2-x+c经过点Q(-1,2),且它的顶点P的横坐标为-1.设抛物线与x轴相交于A、B两点,
已知抛物线y=ax2-x+c经过点Q(-1,2),且它的顶点P的横坐标为-1.设抛物线与x轴相交于A、B两点, 如图,将一副三角板叠放在一起,使直角顶点重合于O,则∠AOC+∠DOB=
如图,将一副三角板叠放在一起,使直角顶点重合于O,则∠AOC+∠DOB=