题目内容
1.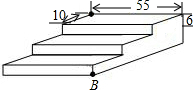 如图是一个三级台阶,它的每一级的长、宽、高分别等于55dm、10dm和6dm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物,则这只蚂蚁从A点出发沿着台阶爬到B点的最短距离是73dm.
如图是一个三级台阶,它的每一级的长、宽、高分别等于55dm、10dm和6dm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物,则这只蚂蚁从A点出发沿着台阶爬到B点的最短距离是73dm.
分析 展开后得到直角三角形ACB,根据题意求出AC、BC,根据勾股定理求出AB即可.
解答  解:展开后由题意得:∠C=90°,AC=3×10+3×6=48,
解:展开后由题意得:∠C=90°,AC=3×10+3×6=48,
BC=55,
由勾股定理得:AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{4{8}^{2}+5{5}^{2}}$=73dm,
故答案为:73.
点评 本题主要考查对勾股定理,平面展开-最短路径问题等知识点的理解和掌握,能理解题意知道是求出直角三角形ABC的斜边AB的长是解此题的关键.

练习册系列答案
相关题目
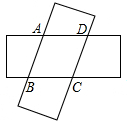 如图用两个完全相同的1cm×4cm长方形纸片,其中心用细铁丝串起来,使纸片交叉叠合,旋转纸片,保持重叠部分形状为菱形,则菱形的最大面积是$\frac{17}{8}$cm2.
如图用两个完全相同的1cm×4cm长方形纸片,其中心用细铁丝串起来,使纸片交叉叠合,旋转纸片,保持重叠部分形状为菱形,则菱形的最大面积是$\frac{17}{8}$cm2.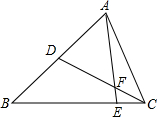 如图,在△ABC中,D是AB的中点,E是BC上的一点,且BE=4EC,CD与AE相交于点F.若△CEF的面积为1,则△ABC的面积为30.
如图,在△ABC中,D是AB的中点,E是BC上的一点,且BE=4EC,CD与AE相交于点F.若△CEF的面积为1,则△ABC的面积为30. 如图,直角梯形ABCD的底边BC的长为20,将它向下平移4个单位得到直角梯形EFGH,测得PC=2,求阴影郁分的面积.
如图,直角梯形ABCD的底边BC的长为20,将它向下平移4个单位得到直角梯形EFGH,测得PC=2,求阴影郁分的面积.