题目内容
9.已知实数x、y满足2x+3y=1.(1)用含有x的代数式表示y;
(2)若实数y满足y>1,求x的取值范围;
(3)若实数x、y满足x>-1,y≥-$\frac{1}{2}$,且2x-3y=k,求k的取值范围.
分析 (1)移项得出3y=1-2x,方程两边都除以3即可;
(2)根据题意得出不等式,求出不等式的解集即可;
(3)解方程组求出x、y,得出不等式组,求出不等式组的解集即可.
解答 解:(1)2x+3y=1,
3y=1-2x,
y=$\frac{1-2x}{3}$;
(2)y=$\frac{1-2x}{3}$>1,
解得:x<-1,
即若实数y满足y>1,x的取值范围是x<-1;
(3)联立2x+3y=1和2x-3y=k得:$\left\{\begin{array}{l}{2x-3y=1}\\{2x+3y=k}\end{array}\right.$,
解方程组得:$\left\{\begin{array}{l}{x=\frac{1+k}{4}}\\{y=\frac{1-k}{6}}\end{array}\right.$,
由题意得:$\left\{\begin{array}{l}{\frac{1+k}{4}>-1}\\{\frac{1-k}{6}≥-\frac{1}{2}}\end{array}\right.$,
解得:-5<k≤4.
点评 本题考查了解二元一次方程和解二元一次方程组、解一元一次不等式组等知识点,能正确解方程组或不等式组是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
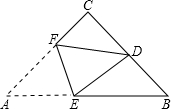 如图,在等腰Rt△ABC中,∠C=90°,D是BC的中点,将△ABC折叠,使A点与D点重合,EF为折痕.
如图,在等腰Rt△ABC中,∠C=90°,D是BC的中点,将△ABC折叠,使A点与D点重合,EF为折痕.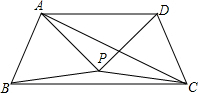 如图,△APB和△DPC是两个全等的等边三角形,AP⊥DP,有以下四个结论:①∠PBC=15°;②AC=BC;③AD∥BC;④直线PC⊥AB,其中正确的结论有①②③④(填序号).
如图,△APB和△DPC是两个全等的等边三角形,AP⊥DP,有以下四个结论:①∠PBC=15°;②AC=BC;③AD∥BC;④直线PC⊥AB,其中正确的结论有①②③④(填序号).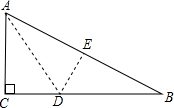 如图,一块直角三角形的纸片,两直角边AC=6cm,BC=8cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合.
如图,一块直角三角形的纸片,两直角边AC=6cm,BC=8cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合.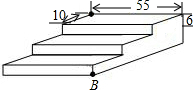 如图是一个三级台阶,它的每一级的长、宽、高分别等于55dm、10dm和6dm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物,则这只蚂蚁从A点出发沿着台阶爬到B点的最短距离是73dm.
如图是一个三级台阶,它的每一级的长、宽、高分别等于55dm、10dm和6dm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物,则这只蚂蚁从A点出发沿着台阶爬到B点的最短距离是73dm.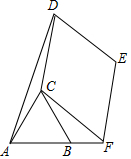 如图,点B在线段AF上,等边三角形ABC边长为1,菱形CDEF边长为$\sqrt{7}$,且∠DCF=120°.则△ACD的面积是$\frac{\sqrt{3}}{2}$.
如图,点B在线段AF上,等边三角形ABC边长为1,菱形CDEF边长为$\sqrt{7}$,且∠DCF=120°.则△ACD的面积是$\frac{\sqrt{3}}{2}$.