题目内容
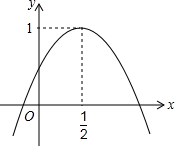 如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(| 1 |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
考点:二次函数图象与系数的关系
专题:数形结合
分析:由抛物线开口方向得到a<0,由抛物线与y轴的交点在x轴上方得到c>0,由抛物线的对称轴为直线x=-
=
,得到b=-a>0,于是可对①进行判断;根据抛物线与x轴交点的各数对②进行判断;根据抛物线的对称性得到抛物线与x轴的另一个交点在(1,0)右边,则x=1时,函数值为正数,于是可对③进行判断;利用抛物线的对称轴得到b=-a,则可对④进行判断;根据抛物线的顶点坐标公式可对⑤进行判断.
| b |
| 2a |
| 1 |
| 2 |
解答:解:∵抛物线开口向下,
∴a<0,
∵抛物线与y轴交于(0,c),
∴c>0,
∵抛物线的对称轴为直线x=-
=
,
∴b=-a>0,
∴abc<0,所以①其中;
∵抛物线与x轴有2个交点,
∴b2-4ac>0,所以②正确;
∵抛物线的对称轴为直线x=
,抛物线与x轴的一个交点在(0,0)的左边,
∴抛物线与x轴的另一个交点在(1,0)右边,
∴x=1时,y>0,
∴a+b+c>0,所以③错误;
∵b=-a,
∴a+b=0,所以④正确;
∵抛物线的顶点坐标为(
,1),
∴
=1,
∴4ac-b2=4a,所以⑤正确.
故选D.
∴a<0,
∵抛物线与y轴交于(0,c),
∴c>0,
∵抛物线的对称轴为直线x=-
| b |
| 2a |
| 1 |
| 2 |
∴b=-a>0,
∴abc<0,所以①其中;
∵抛物线与x轴有2个交点,
∴b2-4ac>0,所以②正确;
∵抛物线的对称轴为直线x=
| 1 |
| 2 |
∴抛物线与x轴的另一个交点在(1,0)右边,
∴x=1时,y>0,
∴a+b+c>0,所以③错误;
∵b=-a,
∴a+b=0,所以④正确;
∵抛物线的顶点坐标为(
| 1 |
| 2 |
∴
| 4ac-b2 |
| 4a |
∴4ac-b2=4a,所以⑤正确.
故选D.
点评:本题考查了二次函数与系数的关系:二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小.当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置,当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异);常数项c决定抛物线与y轴交点,抛物线与y轴交于(0,c).当△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一个不透明的袋中装有5个红球、1个白球,每个球除颜色外均相同,从中任意摸出一个球,则摸出的球是红球的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
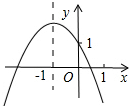 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①a+b+c<0;②b2-4ac>0;③b>0;④4a-2b+c<0;⑤c-a>1,其中正确结论的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①a+b+c<0;②b2-4ac>0;③b>0;④4a-2b+c<0;⑤c-a>1,其中正确结论的是( )| A、①② | B、①③⑤ |
| C、②③⑤ | D、①②⑤ |
某道路一侧原有路灯106盏,相邻两盏灯的距离为36米,现计划全部更换为新型的节能灯,且相邻两盏灯的距离变为70米.设需更换的新型节能灯为x盏,则可列方程( )
| A、70x=106×36 |
| B、70×(x+1)=36×(106+1) |
| C、106-x=70-36 |
| D、70(x-1)=36×(106-1) |
已知a-b=1,则代数式2b-2a的值是( )
| A、-1 | B、1 | C、-2 | D、2 |
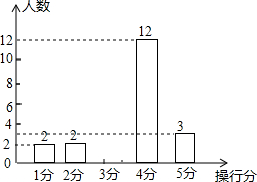 小明所在班级有50名同学,男、女生人数各占一半,在本周操行评定中全班操行得分情况如统计表中所示,如图是该班本周男生操行得分的条形统计图:
小明所在班级有50名同学,男、女生人数各占一半,在本周操行评定中全班操行得分情况如统计表中所示,如图是该班本周男生操行得分的条形统计图: