题目内容
18．若a，b是方程x2+2x-2016=0的两根，则a2+3a+b=（ ）| A． | 2016 | B． | 2015 | C． | 2014 | D． | 2012 |
分析 先根据一元二次方程的解的定义得到a2+2a-2016=0，即a2=-2a+2016，则a2+3a+b可化简为a+b+2016，再根据根与系数的关系得a+b=-2，然后利用整体代入的方法计算．
解答 解：∵a是方程x2+2x-2016=0的实数根，
∴a2+2a-2016=0，
∴a2=-2a+2016，
∴a2+3a+b=-2a+2016+3a+b=a+b+2016，
∵a、b是方程x2+2x-2016=0的两个实数根，
∴a+b=-2，
∴a2+3a+b=-2+2016=2014．
故选：C．
点评 本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1•x2=$\frac{c}{a}$．也考查了一元二次方程的解．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
红果子三级测试卷系列答案
相关题目
如图，正比例函数y=k1x的图象与反比例函数y=$\frac{{k}_{2}}{x}$的图象相交于A，B两点，其中点A的坐标为（$\sqrt{3}$，2$\sqrt{3}$）．
如图，已知AD，AE分别是△ABC的高和中线，AB=6cm，AC=8cm，BC=10cm，∠CAB=90°，求：
如图，△ABC中，AB=AC，以AB为直径的⊙O交BC于D点，DE⊥AC于点E．
10．下列各式成立的是（ ）
| A． | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{23}$ | B． | 2$\sqrt{5}$×3$\sqrt{5}$=6$\sqrt{5}$ | C． | 5$\sqrt{3}$×4$\sqrt{2}$=20$\sqrt{6}$ | D． | 4$\sqrt{3}$×3$\sqrt{2}$=7$\sqrt{5}$ |
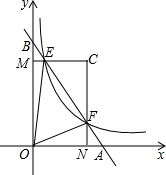在直角坐标系中，直线AB与x轴，y轴分别交于点A，B，与反比例函数y=$\frac{k}{x}$（k为常数，且k＞0）在第一象限的图象交于点E，F，过E作EM⊥y轴于M，过点F作FN⊥x轴于N，直线EM与FN交于点C．