题目内容
17.$\frac{{a}^{3}+1}{1-a+{a}^{2}}$=a+1.分析 先利用立方和公式把分子分解因式,然后约分即可.
解答 解:原式=$\frac{(a+1)({a}^{2}-a+1)}{{a}^{2}-a+1}$=a+1.
故答案为a+1.
点评 本题考查了约分:约去分式的分子与分母的公因式,不改变分式的值,这样的分式变形叫做分式的约分.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.已知R=$\frac{2008×2009}{2010×2011}$,S=$\frac{2008×2010}{2009×2011}$,T=$\frac{2008×2011}{2009×2010}$,则( )
| A. | R>S>T | B. | T>S>R | C. | S>T>R | D. | S>R>T |
 如图,在等腰直角三角形ABC中,点P是斜边AB上的任意一点(不与点A、B重合),试探究PA2+PB2与PC2间的数量关系,并说明理由.
如图,在等腰直角三角形ABC中,点P是斜边AB上的任意一点(不与点A、B重合),试探究PA2+PB2与PC2间的数量关系,并说明理由.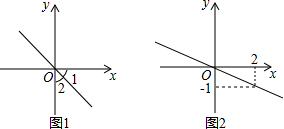 由正比例函数图象写出函数解析式
由正比例函数图象写出函数解析式 如图,A城气象台测得台风中心在A城正西方向300km处,以每小时10$\sqrt{7}$km的速度向北偏东60°的BF方向移动,距台风中心200km的范围内是受台风影响的区域.
如图,A城气象台测得台风中心在A城正西方向300km处,以每小时10$\sqrt{7}$km的速度向北偏东60°的BF方向移动,距台风中心200km的范围内是受台风影响的区域.