题目内容
5.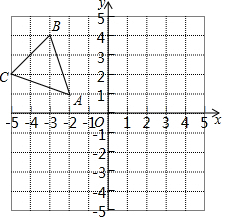 如图,△ABC中,点A(-2,1)、B(-3,4)C(-5,2)均在格点上.在所给直角坐标系中解答下列问题:
如图,△ABC中,点A(-2,1)、B(-3,4)C(-5,2)均在格点上.在所给直角坐标系中解答下列问题:(1)将△ABC平移得△A1B1C1使得点B的对应点B1与原点O重合,在所给直角坐标系中画出图形;
(2)在图中画出△ABC关于y轴对称的△A2B2C2,并写出A2、B2、C2的坐标;
(3)在x轴上找一点P,使得△PAB2的周长最小,请直接写出点P的坐标.
分析 (1)利用平移的性质得出对应点位置,进而得出答案;
(2)直接利用对称图形的性质得出对应点位置进而得出答案;
(3)利用轴对称求最短路线的方法得出答案.
解答  解:(1)如图所示:△A1B1C1,即为所求;
解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求;
A2(2,1),B2(3,4),C2(5,2);
(3)如图所示:得△PAB2的周长最小,P(-1,0).
点评 此题主要考查了平移变换以及轴对称变换和利用轴对称求最短路线,正确得出对应点位置是解题关键.

练习册系列答案
相关题目
15. 如图所示的几何体,从左面看到的形状图是( )
如图所示的几何体,从左面看到的形状图是( )
 如图所示的几何体,从左面看到的形状图是( )
如图所示的几何体,从左面看到的形状图是( )| A. |  | B. |  | C. |  | D. |  |
16.下列英文字母既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
13.如图,在两个形状、大小完全相同的大长方形内,分别互不重叠地放入四个如图③的小长方形后得图①、图②,已知大长方形的长为a,两个大长方形未被覆盖部分分别用阴影表示,则图①阴影部分周长与图②阴影部分周长的差是( )(用a的代数式表示)( )
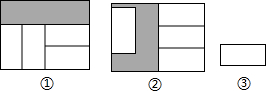

| A. | -a | B. | -$\frac{1}{2}$a | C. | $\frac{1}{2}$a | D. | a |
20.计算(a-2)(-a-2)的结果正确的是( )
| A. | a2-4 | B. | a2-4a+4 | C. | 4-a2 | D. | 2-a2 |
10.若关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根,则k的取值范围是( )
| A. | k>1 | B. | k>-1且k≠0 | C. | k≥-1且k≠0 | D. | k<1且k≠0 |
 如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠ABD=62°,则∠BCD=28°.
如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠ABD=62°,则∠BCD=28°. 如图,在平面直角坐标系中,点A、B、C的坐标分别为(-1,3)、(-4,1)、(-2,1),先将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2,点A1的对应点为点A2.
如图,在平面直角坐标系中,点A、B、C的坐标分别为(-1,3)、(-4,1)、(-2,1),先将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2,点A1的对应点为点A2. 爱动脑筋的小丽同学,为了检验四边形桌面ABCD是否为矩形(如图),她用三角尺量了∠B=∠D=90°,用刻度尺量了AB=CD,就判断四边形桌面ABCD是矩形,请你说明道理.
爱动脑筋的小丽同学,为了检验四边形桌面ABCD是否为矩形(如图),她用三角尺量了∠B=∠D=90°,用刻度尺量了AB=CD,就判断四边形桌面ABCD是矩形,请你说明道理.