题目内容
2．若按一定规律排列的数据如下：$\frac{2}{3}$，-$\frac{5}{8}$，$\frac{10}{15}$，-$\frac{17}{24}$，$\frac{26}{35}$，…，则第n个数可用代数式表示为（-1）n+1•$\frac{{n}^{2}+1}{n（n+2）}$．分析 将数列中每个数分割成3部分：符号、分子、分母，符号的规律是序数为奇数时为正、序数为偶数时为正；分子是序数的平方与1的和；分母是序数与序数加2的乘积，据此可得．
解答 解：∵第1个数$\frac{2}{3}$=（-1）2×$\frac{{1}^{2}+1}{1×（1+2）}$，
第2个数-$\frac{5}{8}$=（-1）3×$\frac{{2}^{2}+1}{2×（2+2）}$，
第3个数$\frac{10}{15}$=（-1）4×$\frac{{3}^{2}+1}{3×（3+2）}$，
…
∴第n个数为：（-1）n+1•$\frac{{n}^{2}+1}{n（n+2）}$，
故答案为：（-1）n+1•$\frac{{n}^{2}+1}{n（n+2）}$．
点评 本题主要考查数字的变化规律，将数列中每个数分割成3部分：符号、分子、分母，分别寻找其与序数的关系是解题的关键．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
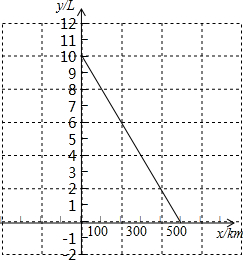某种摩托车的油箱加油满后，油箱中的剩余油量y（L）与摩托车行驶路程x（km）之间的关系如图所示．根据图象回答下列问题：
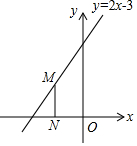如图，点M是直线y=2x+3上的动点，过点M作MN垂直x轴于点N，点P是y轴上的动点，当以M，N，P为顶点的三角形为等腰直角三角形时点M的坐标为（-3，-3）或（-1，1）或（-$\frac{3}{4}$，$\frac{3}{2}$）．
已知实数：-0.$\stackrel{•}{3}$，-$\sqrt{2}$，$\frac{22}{7}$，-$\frac{π}{2}$，4，$\root{3}{{3\frac{3}{8}}}$，2.2121121112…（每两个2之间依次多1个1）