Question

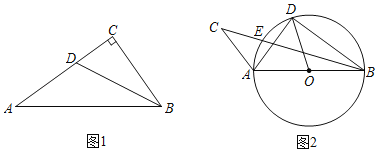
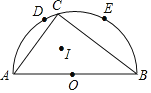
【题目】如图，已知点D，E是半圆O上的三等分点，C是弧DE上的一个动点，连结AC和BC，点I是△ABC的内心，若⊙O的半径为3，当点C从点D运动到点E时，点I随之运动形成的路径长是_____．

Answer 1

【答案】π．

【解析】

连接AI,BI,作OT⊥AB交⊙O 于T,连接AT,TB,以T为圆心,TA为半径作⊙T, 在优弧AB上取一点G,连接AG,BG．证明∠AIB+∠G=180°,推出A,I,B,G四点共圆,

如图，连接AI，BI，作OT⊥AB交⊙O 于T，连接AT，TB，以T为圆心，TA为半径作⊙T，在优弧AB上取一点G，连接AG，BG．推出点I的运动轨迹是即可解决问题．

∵AB是直径,

∴∠ACB＝90°,

∵I是△ABC的内心,

∴∠AIB＝135°,

∵OT⊥AB,OA＝OB,

∴TA＝TB,∠ATB＝90°,

∴∠AGB＝∠ATB＝45°,

∴∠AIB+∠G＝180°,

∴A，I，B，G四点共圆,

∴点I的运动轨迹是,

由题意 ,

∴∠MTM＝30°,易知TA＝TM＝3,

∴点I随之运动形成的路径长是,

故答案为．