��Ŀ����
����Ŀ����֪��![]() ��ֱ��
��ֱ��![]() �����
�����![]() ��ֱ��
��ֱ��![]() �ľ���
�ľ���![]() ���ù�ʽ
���ù�ʽ![]() ���㣮
���㣮
���磺���![]() ��ֱ��
��ֱ��![]() �ľ��룮
�ľ��룮
�⣺��Ϊֱ��![]() ������
������![]() ��
��
���Ե�![]() ��ֱ��
��ֱ��![]() �ľ���Ϊ
�ľ���Ϊ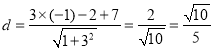 ��
��
�������ϲ��ϣ�����������⣺
��1����![]() ��ֱ��
��ֱ��![]() �ľ��룻
�ľ��룻
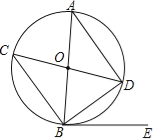
��2����֪![]() ��Բ��
��Բ��![]() ������Ϊ
������Ϊ![]() ���뾶
���뾶![]() Ϊ2���ж�
Ϊ2���ж�![]() ��ֱ��
��ֱ��![]() ��λ�ù�ϵ��˵�����ɣ�
��λ�ù�ϵ��˵�����ɣ�
��3����ֱ֪��![]() ��
��![]() ƽ�У�
ƽ�У�![]() ��
��![]() ��ֱ��
��ֱ��![]() �ϵ�������
�ϵ�������![]() ��
��![]() ��ֱ��
��ֱ��![]() ������һ�㣬��
������һ�㣬��![]() �������
�������
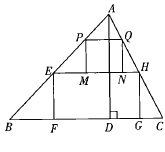
��4����ͼ��ֱ��![]() ��
��![]() �ᡢ
�ᡢ![]() ��ֱ���
��ֱ���![]() ��
��![]() ���㣬��
���㣬��![]() ��ֱ��
��ֱ��![]() ���ۺ�õ�
���ۺ�õ�![]() ����
����![]() �ij���
�ij���
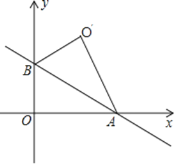
���𰸡���1��![]() ����2��
����2��![]() ��ֱ��
��ֱ��![]() ���У����������������3��
�������������������3��![]() ����4��
����4��![]()
��������
��1�����ݵ㵽ֱ�ߵľ��빫ʽ���뼴�ɣ�
��2�����ݵ㵽ֱ�ߵľ��빫ʽ�������Բ��Q��ֱ��![]() �ľ��룬Ȼ�����ֱ����Բ��λ�ù�ϵ�ж����ɣ�
�ľ��룬Ȼ�����ֱ����Բ��λ�ù�ϵ�ж����ɣ�
��3����ֱ��![]() ��ȡһ��
��ȡһ��![]() �����ݵ㵽ֱ�ߵľ��빫ʽ���������Q��ֱ��
�����ݵ㵽ֱ�ߵľ��빫ʽ���������Q��ֱ��![]() �ľ��룬Ȼ�����ƽ����֮��ľ��봦����Ⱥ������������ʽ���㼴�ɣ�
�ľ��룬Ȼ�����ƽ����֮��ľ��봦����Ⱥ������������ʽ���㼴�ɣ�
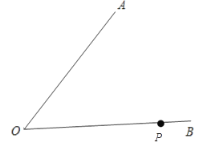
��4������![]() ��AB�ڵ�
��AB�ڵ�![]() �����۵������ʵã�
�����۵������ʵã�![]() ���Ӷ��ó�ֱ��AB��ֱƽ��
���Ӷ��ó�ֱ��AB��ֱƽ��![]() ���ɵ�OM��AB��
���ɵ�OM��AB��![]() ��Ȼ��㵽ֱ�ߵľ��빫ʽ���������O��ֱ��
��Ȼ��㵽ֱ�ߵľ��빫ʽ���������O��ֱ��![]() �ľ���OM�ij����Ӷ����
�ľ���OM�ij����Ӷ����![]() �ij���
�ij���
�⣺��1�����ݵ㵽ֱ�ߵľ��빫ʽ��֪����![]() ��ֱ��
��ֱ��![]() �ľ���
�ľ���![]() ��
��
��2�����ۣ��ж�![]() ��ֱ��
��ֱ��![]() ���У�
����
���ɣ����ݵ㵽ֱ�ߵľ��빫ʽ��֪����![]() ��ֱ��
��ֱ��![]() �ľ���
�ľ��� ��
��
��![]() �İ뾶Ϊ2��
�İ뾶Ϊ2��
��![]() ��
��
��![]() ��ֱ��
��ֱ��![]() ���У�
����
��3����ֱ��![]() ��ȡһ��
��ȡһ��![]() ��
��
���ݵ㵽ֱ�ߵľ��빫ʽ��֪����![]() ����ֱ��
����ֱ��![]() �ľ���
�ľ���![]() ��
��
��ֱ��![]() ��
��![]() ƽ�У�
ƽ�У�
![]() ��
��
��4���⣺��ͼ������![]() ��AB�ڵ�
��AB�ڵ�![]()
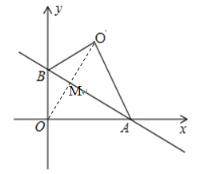
���۵������ʵã�![]() ��
��
��ֱ��AB��ֱƽ��![]()
��OM��AB��![]()
����O��0,0����ֱ��![]() �ľ���OM=
�ľ���OM=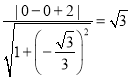
��![]()
��![]() ��
��