Question

19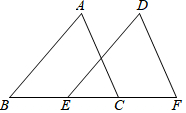．如图，已知点B、E、C、F在同一条直线上，AB=DE，AC=DF，BE=CF．
求证：（1）△ABC≌△DEF；
（2）AB∥DE．

Answer 1

分析 （1）根据三边对应相等两三角形全等即可判定；
（2）欲证明AB∥DE，只要证明∠B=∠DEF．

解答 证明：（1）∵BE=CF，
∴BE+EC=EC+CF，
即BC=EF，
在△ABC和△DEF中，
$\left\{\begin{array}{l}{AB=DE}\\{AC=DF}\\{BC=EF}\end{array}\right.$，
∴△ABC≌△DEF（SSS）．

（2）∵△ABC≌△DEF，
∴∠B=∠DEF，
∴AB∥DE（同位角相等，两直线平行）．

点评 本题考查全等三角形的判定和性质、平行线的判定等知识，解题的关键是正确寻找全等三角形的全等条件，灵活运用所学知识解决问题，属于中考常考题型．