题目内容
13．下列函数中，其图象与x轴有两个交点的是（ ）| A． | y=（x+2015）2+2016 | B． | y=（x-2015）2+2016 | C． | y=-（x-2015）2-2016 | D． | y=-（x+2015）2+2016 |
分析 分别令y=0得到四个一元二次方程，然后通过判断方程实数解的个数确定图象与x轴的交点个数，从而得到正确答案．
解答 解：A、当y=0时，（x+2015）2+2016=0，此方程没有实数解，所以A选项错误；
B、当y=0时，（x-2015）2+2016=0，此方程没有实数解，所以B选项错误；
C、当y=0时，-（x+2015）22-016=0，此方程没有两实数解，所以C选项错误；
D、当y=0时，-（x+2015）2+2016=0，此方程有两个实数解，所以D选项正确．
故选D．
点评 本题考查了抛物线与x轴的交点：二次函数y=ax2+bx+c（a，b，c是常数，a≠0）的交点与一元二次方程ax2+bx+c=0根之间的关系：△=b2-4ac决定抛物线与x轴的交点个数．△=b2-4ac＞0时，抛物线与x轴有2个交点；△=b2-4ac=0时，抛物线与x轴有1个交点；△=b2-4ac＜0时，抛物线与x轴没有交点．
练习册系列答案
学习实践园地系列答案
相关题目
3．下列代数式是最简形式的是（ ）
| A． | $\frac{{{x^2}-4}}{x-2}$ | B． | $\frac{{4{x^2}+4x+1}}{2x+1}$ | C． | $\sqrt{4{x^3}}$ | D． | $\frac{{\sqrt{5}-1}}{2}$ |
4．方程x2+6x+4=0经过配方后，其结果正确的是（ ）
| A． | （x+2）2=0 | B． | （x+3）2=13 | C． | （x+3）2=5 | D． | （x-3）2=5 |
8．下列各数中，是不等式2x+1≥7的解的是（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
18．
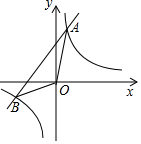如图，点A、B是双曲线y=$\frac{k+1}{x}$（k为正整数）与直线AB的交点，且A、B两点的横坐标是关于x的方程：x2+kx-k-1=0的两根
（1）填表：
（2）当k=n（n为正整数）时，试求直线AB的解析式（用含n的式子表示）；
（3）当k=1、2、3、…n时，△ABO的面积，依次记为S1、S2、S3…Sn，当Sn=40时，求双曲线y=$\frac{k+1}{x}$的解析式．
如图，点A、B是双曲线y=$\frac{k+1}{x}$（k为正整数）与直线AB的交点，且A、B两点的横坐标是关于x的方程：x2+kx-k-1=0的两根（1）填表：
| K | 1 | 2 | 3 | … | n（n为正整数） |
| A点的横坐标 | 1 | 1 | 1 | … | 1 |
| B点的横坐标 | -2 | -3 | -4 | … | -n-1 |
（3）当k=1、2、3、…n时，△ABO的面积，依次记为S1、S2、S3…Sn，当Sn=40时，求双曲线y=$\frac{k+1}{x}$的解析式．
如图：△ABE≌△ACD，∠A=60°，∠B=40°，则∠C=40度．
如图所示，AD∥BC，BO，CO分别平分∠ABC，∠DCB，若∠A+∠D=225°，则∠BOC=112.5度．