题目内容
17. 如图,∠AOB是钝角,OC、OD、OE是三条射线,若OC⊥OA,OD平分∠AOB,OE平分∠BOC,那么∠DOE的度数是45°.
如图,∠AOB是钝角,OC、OD、OE是三条射线,若OC⊥OA,OD平分∠AOB,OE平分∠BOC,那么∠DOE的度数是45°.
分析 设∠BOC=x°,则∠AOB=90°+x°,根据角平分线的定义即可表示出∠BOD和∠BOE的度数,根据∠DOE=∠BOD-∠BOE即可求解.
解答 解:设∠BOC=x°,则∠AOB=90°+x°,
∵OD平分∠AOB,
∴∠BOD=$\frac{1}{2}$(90+x)°,
∵OE平分∠BOC,
∴∠BOE=$\frac{1}{2}$x°,
∴∠DOE=∠BOD-∠BOE=$\frac{1}{2}$(90+x)°-$\frac{1}{2}$x°=45°,
故答案为:45°.
点评 本题考查了角度的计算,正确设出未知数,表示出∠BOD和∠BOE的度数是关键.

练习册系列答案
相关题目
6.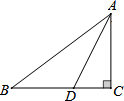 如图,在Rt△ABC中,AD平分∠BAC,AC=BC,∠C=Rt∠,那么$\frac{AC}{DC}$的值为( )
如图,在Rt△ABC中,AD平分∠BAC,AC=BC,∠C=Rt∠,那么$\frac{AC}{DC}$的值为( )
 如图,在Rt△ABC中,AD平分∠BAC,AC=BC,∠C=Rt∠,那么$\frac{AC}{DC}$的值为( )
如图,在Rt△ABC中,AD平分∠BAC,AC=BC,∠C=Rt∠,那么$\frac{AC}{DC}$的值为( )| A. | ($\sqrt{2}$-1):1 | B. | ($\sqrt{2}$+1):1 | C. | $\sqrt{2}$:1 | D. | 2:1 |
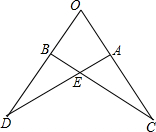 如图,若△OBC≌△OAD,且AC=6,OD=10,则OA=4.
如图,若△OBC≌△OAD,且AC=6,OD=10,则OA=4. 如图,
如图,