题目内容
1.在有理数的范围内,我们定义三个数之间的新运算“#”法则:a#b#c=$\frac{|a-b-c|+a+b+c}{2}$.如:(-1)#2#3=$\frac{|-1-2-3|+(-1)+2+3}{2}$=5
(1)计算:4#(-2)#(-5)=4
(2)计算:3#(-7)#($\frac{11}{3}$)=3
(3)在-$\frac{6}{7}$,-$\frac{5}{7}$,…,-$\frac{1}{7}$,0,$\frac{1}{9}$,$\frac{2}{9}$,…,$\frac{8}{9}$这15个数中:
①任取三个数作为a、b、c的值,进行“a#b#c”运算,求所有计算结果的最小值是-$\frac{11}{7}$;
②若将这十五个数任意分成五组,每组三个数,进行“a#b#c”运算,得到五个不同的结果,由于分组不同,所以五个运算的结果也不同,那么五个结果之和的最大值是4.
分析 (1)、(2)根据题中所给出的例子列式计算即可;
(3)分a<b+c与a≥b+c两种情况求出原式的值,
①令b=-$\frac{6}{7}$,c=-$\frac{5}{7}$即可得出最小值;
②将$\frac{1}{9}$,$\frac{2}{9}$…$\frac{8}{9}$分别赋予b,c,同时赋予a四个负数,最后一组a=0,b,c赋予两个负数即可.
解答 解:(1)原式=$\frac{|4+2+5|+4-2-5}{2}$=$\frac{8}{2}$=4.
故答案为:4;
(2)原式=$\frac{|3+7-\frac{11}{3}|+3-7+\frac{11}{3}}{2}$=3.
故答案为:3;
(3)①当a=b+c时,原式的值最小,
令b=-$\frac{5}{7}$,c=-$\frac{1}{7}$,则原式最小值=-$\frac{5}{7}$-$\frac{1}{7}$=-$\frac{6}{7}$;
故答案为:-$\frac{6}{7}$;
②∵当a=-$\frac{6}{7}$,b=$\frac{1}{9}$,c=$\frac{2}{9}$,则原式=$\frac{1}{9}$+$\frac{2}{9}$=$\frac{1}{3}$;
当a=-$\frac{5}{7}$,b=$\frac{3}{9}$,c=$\frac{4}{9}$,则原式=$\frac{3}{9}$+$\frac{4}{9}$=$\frac{7}{9}$;
当a=-$\frac{4}{7}$,b=$\frac{5}{9}$,c=$\frac{6}{9}$,则原式=$\frac{5}{9}$+$\frac{6}{9}$=$\frac{11}{9}$;
当a=-$\frac{3}{7}$,b=$\frac{7}{9}$,c=$\frac{8}{9}$,则原式=$\frac{7}{9}$+$\frac{8}{9}$=$\frac{15}{9}$;
当a=0,b=-$\frac{1}{7}$,c=-$\frac{2}{7}$,原式=0,
∴五个结果之和的最大值=$\frac{1}{3}$+$\frac{7}{9}$+$\frac{11}{9}$+$\frac{15}{9}$=4.
故答案为:4.
点评 本题考查的是有理数的加减混合运算,根据题意列出有理数相加减的式子是解答此题的关键.

| A. | 增加几次实验,事件发生的频率与这一事件发生的概率的差距可能扩大 | |
| B. | 增加几次实验,事件发生的频率越来越接近这一事件发生的概率的差距可能缩小 | |
| C. | 实验次数很大时,事件发生的频率稳定在这一事件发生的概率附近 | |
| D. | 实验次数增大时,事件发生的频率越来越接近这一事件发生的概率 |
| A. | y=x2-(x-1)x | B. | y+ax2=-3 | C. | x2=2y+3 | D. | y=x2+x-2 |
| A. | 等腰三角形 | B. | 直角三角形 | ||
| C. | 等腰直角三角形 | D. | 等腰三角形或直角三角形 |
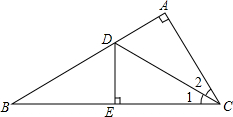 如图,在Rt△ABC中,∠BAC=90°,DE⊥BC,BE=EC,∠1=∠2,AC=6,AB=10,则△BDE的周长是( )
如图,在Rt△ABC中,∠BAC=90°,DE⊥BC,BE=EC,∠1=∠2,AC=6,AB=10,则△BDE的周长是( )