题目内容
如图,在□ABCD中,∠ABC、∠BCD的平分线BE、CF分别与AD相交于点E、F,BE与CF相交于点G.
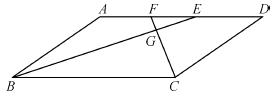
(1)求证:BE⊥CF;
(2)若AB=3,BC=5,CF=2,求BE的长.
(1)证明:∵BE平分∠ABC,
∴∠CBE= ∠ABC.
∠ABC.
同理∠BCF= ∠BCD.
∠BCD.
∵四边形ABCD是平行四边形,∴AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠CBE+∠BCF= ∠ABC+
∠ABC+ ∠BCD=
∠BCD= (∠ABC+∠BCD)=90°,
(∠ABC+∠BCD)=90°,
∴∠CGB=90°,即BE⊥CF.
(2)过点E作EP∥FC,交BC的延长线于点P,则四边形CPEF是平行四边形.
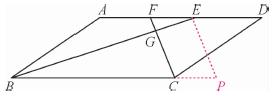
∵BE平分∠ABC,∴∠ABE=∠CBE.
在□ABCD中,∵AD∥BC,∴∠AEB=∠CBE,
∴∠ABE=∠AEB,∴AE=AB=3.
同理DF=DC=3.
∴EF=AE+DF-AD=1,
∴CP=EF=1,EP=CF=2,BP=6.
又由(1)已证得BE⊥CF,∴BE⊥EP,
∴在Rt△BPE中,BE=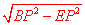 =
=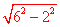 =4
=4 .
.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目


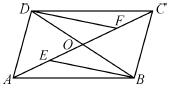
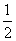 AC,则四边形ABCD是什么特殊四边形?请证明你的结论.
AC,则四边形ABCD是什么特殊四边形?请证明你的结论.