题目内容
如图，四边形ABCD的对角线AC、BD交于点O，已知O是AC的中点，AE=CF，DF∥BE.
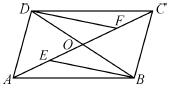
(1)求证：△BOE≌△DOF；
(2)若OD=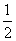
AC，则四边形ABCD是什么特殊四边形？请证明你的结论.
(1)证明：∵O是AC的中点，∴OA=OC.
∵AE=CF，∴OE=OF.
∵DF∥BE，∴∠OEB=∠OFD.
∵∠EOB=∠FOD，
∴△BOE≌△DOF(ASA).
(2)四边形ABCD是矩形.证明如下：
∵△
BOE≌△DOF，∴OD=OB.
∵OA=OC，∴四边形ABCD是平行四边形.
∵OD=
AC，OD=BD，∴AC=BD，
∴四边形ABCD是矩形.
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
-2|-
+(
)-1.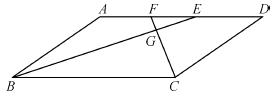
点C，D，则直线CD即为所求.连接AC，BC，AD，BD，根据她的作图方法可知四边形ADBC一定是( )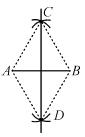
，则正方形ABCD的周长为 .
B.弧是半圆
