题目内容
设x1,x2是方程x2-x-1=0的两个根,则代数式x13+2x2+x1•x2的值为 .
考点:根与系数的关系
专题:计算题
分析:先根据根与系数的关系得到x1+x2=1,x1x2=-1,再利用x1是方程x2-x-1=0的根得到x12-x1-1=0,则x12=x1+1,接着变形得到x13=2x1+1,则x13+2x2+x1•x2=2(x1+x2)+2x1x2,然后利用整体代入得方法计算.
解答:解:根据题意得x1+x2=1,x1x2=-1,
∵x1是方程x2-x-1=0的根,
∴x12-x1-1=0,
∴x12=x1+1,
∴x13=x1(x1+1)=x12+x1=x1+1+x1=2x1+1,
∴x13+2x2+x1•x2=2x1+1+2x2+x1•x2=2(x1+x2)+2x1x2=2×1+2×(-1)=0.
故答案为0.
∵x1是方程x2-x-1=0的根,
∴x12-x1-1=0,
∴x12=x1+1,
∴x13=x1(x1+1)=x12+x1=x1+1+x1=2x1+1,
∴x13+2x2+x1•x2=2x1+1+2x2+x1•x2=2(x1+x2)+2x1x2=2×1+2×(-1)=0.
故答案为0.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.也考查了一元二次方程解的定义.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
如果2是方程x2-a=0的一个根,则a的值是( )
| A、2 | ||
| B、4 | ||
| C、-4 | ||
D、
|
 如图,点A是直线l外一点,在l上任取两点B、C,以A为圆心,以BC长为半径画弧,以C为圆心,以AB长为半径画弧,两弧交于点D,连接AB、AD、CD,则四边形ABCD一定是( )
如图,点A是直线l外一点,在l上任取两点B、C,以A为圆心,以BC长为半径画弧,以C为圆心,以AB长为半径画弧,两弧交于点D,连接AB、AD、CD,则四边形ABCD一定是( )| A、正方形 | B、矩形 |
| C、菱形 | D、平行四边形 |
若分式
的值为零,则x的值为( )
| |x|-1 |
| x-1 |
| A、±1 | B、-1 | C、1 | D、不存在 |
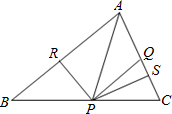 如图,在△ABC中,AQ=PQ,PR=PS,若PR⊥AB,PS⊥AC,垂足分别为点R、S,下列三个结论:①AS=AR;②QP∥AR;③△BPR≌△QPS,其中正确的是( )
如图,在△ABC中,AQ=PQ,PR=PS,若PR⊥AB,PS⊥AC,垂足分别为点R、S,下列三个结论:①AS=AR;②QP∥AR;③△BPR≌△QPS,其中正确的是( )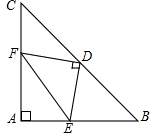 如图,在等腰Rt△ABC中,∠A=90°,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.
如图,在等腰Rt△ABC中,∠A=90°,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.