题目内容
如图1,l1,l2,l3,l4是一组平行线,相邻2条平行线间的距离都是1个单位长度,正方形ABCD的4个顶点A,B,C,D都在这些平行线上.过点A作AF⊥l3于点F,交l2于点H,过点C作CE⊥l2于点E,交l3于点G.
(1)求证:△ADF≌△CBE;
(2)求正方形ABCD的面积;
(3)如图2,如果四条平行线不等距,相邻的两条平行线间的距离依次为h1,h2,h3,试用h1,h2,h3
表示正方形ABCD的面积S.
解:(1)证明:在Rt△AFD和Rt△CEB中,
∵AD=BC,AF=CE,∴Rt△AFD≌Rt△CEB(HL)。
(2)∵∠ABH+∠CBE=90°,∠ABH+∠BAH=90°,∴∠CBE=∠BAH。
又∵AB=BC,∠AHB=∠CEB=90°,∴△ABH≌△BCE(AAS)。
同理可得,△ABH≌△BCE≌△CDG≌△DAF。
∴S正方形ABCD=4S△ABH+S正方形HEGF=4× ×2×1+1+1=5。
×2×1+1+1=5。
(3)由(1)知,△AFD≌△CEB,故h1=h3,
由(2)知,△ABH≌△BCE≌△CDG≌△DAF,
∴S正方形ABCD=4S△ABH+S正方形HEGF=4× (h1+h2)•h1+h22=2h12+2h1h2+h22.
(h1+h2)•h1+h22=2h12+2h1h2+h22.
解析

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
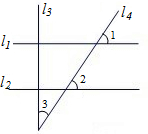 21、如图,直线l1、l2均被直线l3、l4所截,且l3与l4相交,给定以下三个条件:
21、如图,直线l1、l2均被直线l3、l4所截,且l3与l4相交,给定以下三个条件: 如图,直线l1和l2相交于点A(-1,2)且S△AOB=
如图,直线l1和l2相交于点A(-1,2)且S△AOB= 9、如图,直线l1、l2、l3交于O点,图中出现了几对对顶角,若n条直线相交呢?
9、如图,直线l1、l2、l3交于O点,图中出现了几对对顶角,若n条直线相交呢? 如图,直线l1与l2相交于点O,AO⊥l1,若∠1=50°,则∠2的度数为
如图,直线l1与l2相交于点O,AO⊥l1,若∠1=50°,则∠2的度数为 如图两线段l1,l2被直线l3所截,图中同位角的对数与内错角的对数的和是
如图两线段l1,l2被直线l3所截,图中同位角的对数与内错角的对数的和是