题目内容
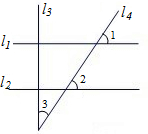 21、如图,直线l1、l2均被直线l3、l4所截,且l3与l4相交,给定以下三个条件:
21、如图,直线l1、l2均被直线l3、l4所截,且l3与l4相交,给定以下三个条件:①l1⊥l3;②∠1=∠2;③∠2+∠3=90°;请从这三个条件中选择两个作为条件,另一个作为结论组成一个真命题,并进行证明
已知:
求证:
证明:
分析:如果选择①②两个作为条件,③作为结论可组成一个真命题.首先根据平行线的判定定理,可得l1∥l2,由l1⊥l3,可得l2⊥l3,然后,根据直角三角形的两个锐角互余及对顶角的性质,即可证明.
解答: 已知:l1⊥l3,∠1=∠2,求证:∠2+∠3=90°.
已知:l1⊥l3,∠1=∠2,求证:∠2+∠3=90°.
证明:∵∠1=∠2,
∴l1∥l2,
∵l1⊥l3,
∴l2⊥l3,
∴∠3+∠4=90°,
∵∠4=∠2,
∴∠2+∠3=90°.
 已知:l1⊥l3,∠1=∠2,求证:∠2+∠3=90°.
已知:l1⊥l3,∠1=∠2,求证:∠2+∠3=90°.证明:∵∠1=∠2,
∴l1∥l2,
∵l1⊥l3,
∴l2⊥l3,
∴∠3+∠4=90°,
∵∠4=∠2,
∴∠2+∠3=90°.
点评:本题主要考查了平行线的判定与性质,注意平行线的性质和判定定理的综合运用.

练习册系列答案
相关题目
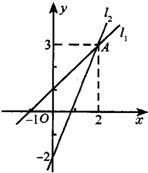 -2),结合图象解答下列问题:
-2),结合图象解答下列问题: 4、如图,直线l1,l2,l3相交于一点,则下列答案中,全对的一组是( )
4、如图,直线l1,l2,l3相交于一点,则下列答案中,全对的一组是( ) 如图,直线l1与l2相交于点O,OM⊥l1,若∠α=44°,则∠β等于
如图,直线l1与l2相交于点O,OM⊥l1,若∠α=44°,则∠β等于 如图,直线l1、l2、l3分别过正方形ABCD的三个顶点A,B,D,且相互平行,若l1与l2的距离为1,l2与l3的距离为1,则该正方形的面积是
如图,直线l1、l2、l3分别过正方形ABCD的三个顶点A,B,D,且相互平行,若l1与l2的距离为1,l2与l3的距离为1,则该正方形的面积是 如图,直线l1与l2相交于点P,l1的函数表达式y=kx+b,且经过(1,7)和(-3,-1)两点,点P的横坐标为-1,且l2交y轴于点A(0,-1).
如图,直线l1与l2相交于点P,l1的函数表达式y=kx+b,且经过(1,7)和(-3,-1)两点,点P的横坐标为-1,且l2交y轴于点A(0,-1).