题目内容
抛物线y=x2-4x+7的顶点坐标为（ ）
| A、（-2，3） |
| B、（-2，-3） |
| C、（2，-3） |
| D、（2，3） |
考点：二次函数的性质
专题：
分析：将抛物线的一般式配方成为顶点式，可求出顶点坐标．
解答：解：∵y=x2-4x+7=（x-2）2+3，
∴抛物线的顶点坐标为（2，3）．
故选D．
∴抛物线的顶点坐标为（2，3）．
故选D．
点评：本题考查了二次函数的顶点式与顶点坐标的关系．顶点式y=（x-h）2+k，顶点坐标为（h，k）．
练习册系列答案
阅读快车系列答案
相关题目
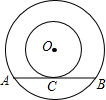如图，以O为圆心的两个同心圆中，大圆的弦AB与小圆相切于点C，若大圆半径为10cm，小圆半径为6cm，则弦AB的长为（ ）| A、2cm | B、4cm |
| C、8cm | D、16cm |
若反比例函数y=
（k≠0）的图象经过点P（-2，3），则该函数的图象的点是（ ）
| k |
| x |
| A、（3，-2） |
| B、（1，-6） |
| C、（-1，6） |
| D、（-1，-6） |
已知一元二次方程x2-4=0，则下列关于它的说法正确的是（ ）
| A、不是一般形式 |
| B、一次项系数是0 |
| C、常数项是4 |
| D、没有二次项系数 |