题目内容
4.已知点P是以AB为直径的圆上一动点,AB=2,设弦AP为x,△APO面积为y,求y关于x的函数关系式.分析 首先由垂径定理可知AC=$\frac{1}{2}x$,然后由勾股定理求得OC的长,最后根据三角形的面积公式求得关系式即可.
解答 解:如图所示,过点O作OC⊥AP,垂足为C.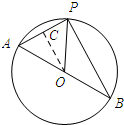
∵OC⊥AP,
∴AC=$\frac{1}{2}AP$=$\frac{1}{2}x$.
在Rt△AOC中,由勾股定理得:OC=$\sqrt{A{O}^{2}-A{C}^{2}}$=$\sqrt{1-\frac{1}{4}{x}^{2}}$.
由三角形的面积公式可知:y=$\frac{1}{2}AP•OC$=$\frac{1}{2}x•\sqrt{1-\frac{1}{4}{x}^{2}}$=$\frac{x\sqrt{4-{x}^{2}}}{4}$.
整理得:y=$\frac{x\sqrt{4-{x}^{2}}}{4}$.
点评 本题主要考查的是勾股定理、垂径定理、三角形的面积公式的应用,求得OC的长是解题的关键.

练习册系列答案
相关题目
16.若a是有理数,则整式a(a-2)-2a+5的值为( )
| A. | 不是负数 | B. | 恒为正数 | C. | 恒为负数 | D. | 不等于零 |
 已知:如图,∠1=∠3,∠2=∠3.求证:AB∥CD.
已知:如图,∠1=∠3,∠2=∠3.求证:AB∥CD.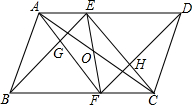 如图,在?ABCD中,过对角线AC的中点O作直线E,F分别与AD,BC交于点E,F,连接BE,AF相交于点G,连结EC,FD相交于点H,图中有几个平行四边形,为什么?
如图,在?ABCD中,过对角线AC的中点O作直线E,F分别与AD,BC交于点E,F,连接BE,AF相交于点G,连结EC,FD相交于点H,图中有几个平行四边形,为什么?