题目内容
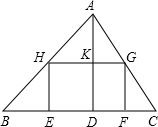△ABC为锐角三角形，AD是边BC上的高，正方形EFGH的一边EF在BC上，顶点G，H分别在AC，AB上，BC=30，AD=20．求这个正方形的边长．考点：相似三角形的判定与性质
专题：
分析：由正方形的性质可知HG∥BC，利用平行线分线段成比例可得
=
，设正方形的边长为x，则AK=20-x，HG=x，代入求出x即可．
| AK |
| AD |
| HG |
| BC |
解答：解：∵四边形EFGH为正方形，
∴HG∥BC，
∴
=
，
设正方形的边长为x，则AK=20-x，HG=x，
∴
=
，
解得x=12，
即正方形EFGH的边长为12．
∴HG∥BC，
∴
| AK |
| AD |
| HG |
| BC |
设正方形的边长为x，则AK=20-x，HG=x，
∴
| 20-x |
| 20 |
| x |
| 30 |
解得x=12，
即正方形EFGH的边长为12．
点评：本题主要考查平行线分线段成比例的性质，掌握平行线分线段成比例中的对应线段是解题的关键，注意方程思想的运用．
练习册系列答案
阅读快车系列答案
相关题目
等边三角形ABC中，AD是高，∠ABC的平分线BH交AD于点O，E是AC边上的点，F是BC边上的点，且△OEF为等边三角形
如图是一个我们喜欢玩的魔方，它是由若干个小正方体组成的一个大正方体，在这个大正方体的六个面上，分别涂有6种不同的颜色，根据你的观察与想象，回答下列问题：
如图，四边形BDEF内接于圆O中，分别延长DE、BF交于点C，直径AB⊥DE于点H．求证：∠1=∠2．一个多边形的内角和等于1440°，则它是（ ）边形．
| A、11 | B、6 | C、5 | D、8 |