题目内容
4.下列计算错误的是( )| A. | $\sqrt{14}$×$\sqrt{7}$=7$\sqrt{2}$ | B. | $\sqrt{60}$÷$\sqrt{5}$=2$\sqrt{3}$ | C. | $\sqrt{25a}$+$\sqrt{9a}$=8$\sqrt{a}$ | D. | 3$\sqrt{2}$-$\sqrt{2}$=3 |
分析 根据二次根式的乘法法则对A进行判断;根据二次根式的除法法则对B进行判断;根据二次根式的加减法对C、D进行判断.
解答 解:A、原式=$\sqrt{2×7}$×$\sqrt{7}$=7$\sqrt{2}$,所以A选项的计算正确;
B、原式=$\sqrt{60÷5}$=$\sqrt{12}$=2$\sqrt{3}$,所以B选项的计算正确;
C、原式=5$\sqrt{a}$+3$\sqrt{a}$=8$\sqrt{a}$,所以C选项的计算正确;
D、原式=2$\sqrt{2}$,所以D选项的计算错误.
故选D.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
15.$\frac{\sqrt{2}}{2}$,38,0,π,$\sqrt{16}$,$\frac{1}{3}$,0.1010010001…(相连两个1之间依次多一个0),其中无理数有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
12.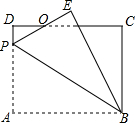 如图,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为( )
如图,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为( )
 如图,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为( )
如图,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为( )| A. | 4.8 | B. | 3$\sqrt{2}$ | C. | 5 | D. | 3$\sqrt{3}$ |
19.下面的实数中是无理数的个数是( )
-0.4,π,-|-4|,0,-$\frac{22}{7}$,-$\sqrt{9}$,$\sqrt{5}$,$\root{3}{\frac{1}{27}}$,4.262262226…(两个6之间依次增加一个“2”)
-0.4,π,-|-4|,0,-$\frac{22}{7}$,-$\sqrt{9}$,$\sqrt{5}$,$\root{3}{\frac{1}{27}}$,4.262262226…(两个6之间依次增加一个“2”)
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.由$\frac{4y-3x}{2}=1$,可以得到用y表示x的式子( )
| A. | y=$\frac{3x-2}{4}$ | B. | 3x=4y-2 | C. | x=$\frac{4y-2}{3}$ | D. | x=$\frac{2-4y}{3}$ |

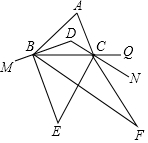 如图,在△ABC中,∠A=68°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别
如图,在△ABC中,∠A=68°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别