题目内容
14.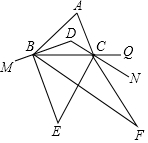 如图,在△ABC中,∠A=68°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别
如图,在△ABC中,∠A=68°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F=14°.
分析 根据三角形的内角和得到∠ABC+∠ACB=180°-∠A=112°,根据角平分线的定义得到∠DBC+∠DCB=$\frac{1}{2}$×112°=56°,根据平角的定义得到∠MBC+∠NCB=360°-56°=304°,由角平分线的定义得到∠CBE+∠BCE=$\frac{1}{2}$(∠MBC+∠NCB)=152°,求得∠E=360°-∠D-∠DBE-∠DCE=28°,根据外角的性质即可得到结论.
解答 解:∵∠A=68°,
∴∠ABC+∠ACB=180°-∠A=112°,
∵BD、CD分别平分∠ABC、∠ACB,
∴∠DBC+∠DCB=$\frac{1}{2}$×112°=56°,
∵∠D=180°-(∠DBC+∠DCB)=124°,
∴∠MBC+∠NCB=360°-56°=304°,
∵BE、CE分别平分∠MBC、∠BCN,
∴∠CBE+∠BCE=$\frac{1}{2}$(∠MBC+∠NCB)=152°,
∴∠E=360°-∠D-∠DBE-∠DCE=28°,
∵BF、CF分别平分∠EBC、∠ECQ,
∴∠QCF=$\frac{1}{2}∠$QCE,∠CBF=$\frac{1}{2}∠$CBE,
∵∠QCE=∠CBE+∠E,∠QCF=∠CBF+∠F,
∴$\frac{1}{2}$(∠CBE+∠E)=$\frac{1}{2}∠$CBE+∠F,
∴∠F=$\frac{1}{3}∠$E=14°,
故答案为:14°.
点评 本题考查了三角形的内角和,三角形的外角的性质,角平分线的定义,熟练掌握外角的性质是解题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
4.下列计算错误的是( )
| A. | $\sqrt{14}$×$\sqrt{7}$=7$\sqrt{2}$ | B. | $\sqrt{60}$÷$\sqrt{5}$=2$\sqrt{3}$ | C. | $\sqrt{25a}$+$\sqrt{9a}$=8$\sqrt{a}$ | D. | 3$\sqrt{2}$-$\sqrt{2}$=3 |
3.反比例函数的图象经过A(-5,y1)、B(-3,y2)、C(-1,3)、D(2,y3),则y1、y2、y3的大小关系是( )
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y1<y2 | D. | y3<y2<y1 |
 如图,反比例函数y=$\frac{3}{x}$的图象与一次函数y=x+2的图象交于A、B两点.当x为-3<x<0或x>1时,反比例函数的值小于一次函数的值.
如图,反比例函数y=$\frac{3}{x}$的图象与一次函数y=x+2的图象交于A、B两点.当x为-3<x<0或x>1时,反比例函数的值小于一次函数的值.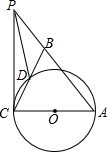 如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于D,P是AB延长线上一点,连PC,且∠PCB=$\frac{1}{2}$∠BAC
如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于D,P是AB延长线上一点,连PC,且∠PCB=$\frac{1}{2}$∠BAC