题目内容
2.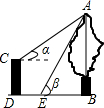 学习完解直角三角形知识,同学们利用它求我校某平房前一棵大树的高度,如图,大树AB与平房CD底部在同一平地,知道二层平房CD高为6米,在平房顶部点C测得树顶A点的仰角α=30°,从平房底部向树的方向水平前进2米到达点E,在点E处测得大树顶A的仰角β=60°,请你帮同学们求出这棵大树高度AB(结果保留根号)
学习完解直角三角形知识,同学们利用它求我校某平房前一棵大树的高度,如图,大树AB与平房CD底部在同一平地,知道二层平房CD高为6米,在平房顶部点C测得树顶A点的仰角α=30°,从平房底部向树的方向水平前进2米到达点E,在点E处测得大树顶A的仰角β=60°,请你帮同学们求出这棵大树高度AB(结果保留根号)
分析 作CF⊥AB于点F,设AF=x米,在直角△ACF中利用三角函数用x表示出CF的长,在直角△ABE中表示出BE的长,然后根据CF-BE=DE即可列方程求得x的值,进而求得AB的长.
解答  解:作CF⊥AB于点F,设AF=x米,
解:作CF⊥AB于点F,设AF=x米,
在Rt△ACF中,tan∠ACF=$\frac{AF}{CF}$,
则CF=$\frac{AF}{tan∠ACF}$=$\frac{x}{tanα}$=$\frac{x}{tan30°}$=$\sqrt{3}$x,
在直角△ABE中,AB=x+BF=6+x(米),
在直角△ABF中,tan∠AEB=$\frac{AB}{BE}$,则BE=$\frac{AB}{tan∠AEB}$=$\frac{x+6}{tan60°}$=$\frac{\sqrt{3}}{3}$(x+6)米.
∵CF-BE=DE,即$\sqrt{3}$x-$\frac{\sqrt{3}}{3}$(x+6)=2.
解得:x=$\frac{\sqrt{3}+9}{3}$,
则AB=$\frac{\sqrt{3}+9}{3}$+6=$\frac{\sqrt{3}+27}{3}$(米).
答:树高AB是$\frac{\sqrt{3}+27}{3}$米.
点评 本题考查了解直角三角形的应用,解答本题关键是构造直角三角形,利用三角函数的知识表示出相关线段的长度.

练习册系列答案
相关题目
17.2017年2月3日,据海关统计,2016年我国货物贸易进出口总值近24万亿元人民币,24万亿元用科学记数法表示为( )
| A. | 2.4×1013元 | B. | 240000×108元 | C. | 24×1012元 | D. | 24×108元 |
14.若关于x的不等式(a-5)x>2a-10的解集是x<2,则a的取值范围是( )
| A. | a<5 | B. | a>5 | C. | a<0 | D. | a>0 |
 把一张对边互相平行的纸条,折成如图所示,EF是折痕.若∠EFB=35°,则下面五个结论:①∠CEF=35°;②∠AEC=145°;③∠BGE=70°;④∠EFD′=110°;⑤∠D′FD=70°.其中正确的是①③⑤.(只填序号)
把一张对边互相平行的纸条,折成如图所示,EF是折痕.若∠EFB=35°,则下面五个结论:①∠CEF=35°;②∠AEC=145°;③∠BGE=70°;④∠EFD′=110°;⑤∠D′FD=70°.其中正确的是①③⑤.(只填序号)
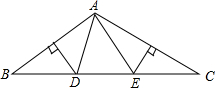 如图,在△ABC中,AB边垂直平分线交BC于点D,AC边垂直平分线交BC于点E,连接AD,AE.
如图,在△ABC中,AB边垂直平分线交BC于点D,AC边垂直平分线交BC于点E,连接AD,AE.