题目内容
2．在六张卡片上分别写有π，$\frac{1}{3}$，1.5，-3，0，$\sqrt{2}$六个数，从中任意抽取一张，卡片上的数为无理数的概率是$\frac{1}{3}$．分析 由π，$\frac{1}{3}$，1.5，-3，0，$\sqrt{2}$六个数中，无理数为：π，$\sqrt{2}$，直接利用概率公式求解即可求得答案．
解答 解：∵π，$\frac{1}{3}$，1.5，-3，0，$\sqrt{2}$六个数中，无理数为：π，$\sqrt{2}$，
∴从中任意抽取一张，卡片上的数为无理数的概率是：$\frac{2}{6}$=$\frac{1}{3}$．
故答案为：$\frac{1}{3}$．
点评 此题考查了概率公式的应用．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案
相关题目
13．
在如图所示的平面直角坐标系中，一只蚂蚁从A点出发，沿着A-B-C-D-A…循环爬行，其中A点坐标为（-1，1），B的坐标为（-1，-1），C的坐标为（-1，3），D的坐标为（1，3），当蚂蚁爬了2015个单位时，它所处位置的坐标为（ ）
在如图所示的平面直角坐标系中，一只蚂蚁从A点出发，沿着A-B-C-D-A…循环爬行，其中A点坐标为（-1，1），B的坐标为（-1，-1），C的坐标为（-1，3），D的坐标为（1，3），当蚂蚁爬了2015个单位时，它所处位置的坐标为（ ）| A． | （1，1） | B． | （1，0） | C． | （0，1） | D． | （1，-1） |
10．下列方程中是一元二次方程的是（ ）
| A． | 2+$\frac{5}{{x}^{2}}$=0 | B． | x+2y=3 | C． | 3x=2x2-1 | D． | x2-3y+2=0 |
如图．已知点A（1，2）、B（4，1）、C（8，3）．利用坐标网格和你的观察力．请直按说出△ABC外心的坐标和外接圆半径．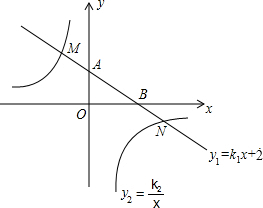
在平面直角坐标系xOy中，一次函数y1=k1x+2的图象与y轴交于点A，与x轴交于点B，与反比例函数y2=$\frac{k_2}{x}$的图象分别交于点M、N，已知△AOB的面积为3，点M的纵坐标为4．
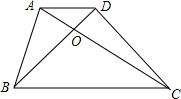如图所示，梯形ABCD中，AD∥BC，对角线AC和BD相交于点O，若S△AOD：S△ACD=1：3．求S△AOD：S△BOC．