题目内容
17．从下面3个方程中选择一个有解的方程，并求出你选择的方程的解．①x2+1=0 ②（3x+2）2-4x2=0 ③3x2-6x+4=0，你选择的方程是②（填相应方程的序号）分析 直接利用根的判别式判断得出方程根的情况，再利用因式分解法解方程得出即可．
解答 解：①x2+1=0
∵b2-4ac=-4＜0，
∴此方程无实数根；
②（3x+2）2-4x2=0，
[（3x+2）-2x]（3x+2+2x）=0，
（x+2）（5x+2）=0，
解得：x1=-2，x2=-$\frac{2}{5}$；
③3x2-6x+4=0
∵b2-4ac=36-4×3×4=-12＜0，
∴此方程无实数根；
故答案为：②．
点评 此题主要考查了因式分解法解方程以及根的判别式，正确应用平方差公式是解题关键．
练习册系列答案
相关题目
7．-2的相反数是（ ）
| A． | .-2 | B． | 2 | C． | -$\frac{1}{2}$ | D． | -$\frac{4}{5}$ |
12．把一元二次方程6x2-3=4x（2x-1）化为一般形式是（ ）
| A． | -2x2-4x+3=0 | B． | 2x2+4x-3=0 | C． | 2x2-4x+3=0 | D． | 2x2-4x-3=0 |
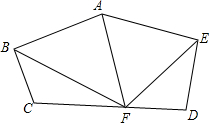如图，已知AB=AE，BC=ED，∠C=∠D，点F是CD的中点，∠BAF与∠EAF相等吗？为什么？