题目内容
16.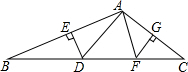 如图,△ABC中,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.
如图,△ABC中,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.(1)如果BC=8,求△DAF的周长.
(2)如果∠BAC=110°,求∠DAF的度数.
分析 (1)根据线段垂直平分线的性质得到DA=DB,FA=FC,根据三角形的周长公式计算即可;
(2)根据三角形内角和定理得到∠B+∠C=70°,根据线段垂直平分线的性质得到DA=DB,FA=FC,得到∠BAD=∠B,∠CAF=∠C,计算即可.
解答 解:(1)∵DE、FG分别为AB、AC的垂直平分线,
∴DA=DB,FA=FC,
∴△DAF的周长=AD+DF+AF=BD+DF+FC=BC=8;
(2)∵∠BAC=110°,
∴∠B+∠C=70°,
∵DA=DB,FA=FC,
∴∠BAD=∠B,∠CAF=∠C,
∴∠BAD+∠CAF=70°,
∴∠DAF=110°-70°=40°.
点评 本题考查的是线段垂直平分线的性质、三角形内角和定理,掌握线段垂直平分线上任意一点,到线段两端点的距离相等是解题的关键.

练习册系列答案
相关题目
4.反比例函数y=$\frac{6}{x}$的图象在( )
| A. | 第一、三象限 | B. | 第一、二象限 | C. | 第二、四象限 | D. | 第三、四象限 |
1.若∠1与∠2是内错角,且∠1=60°,则∠2是( )
| A. | 60° | B. | 120° | C. | 120°或60° | D. | 不能确定 |
5.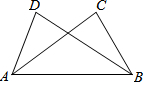 如图,△ABC≌△BAD,点A和点B,点C和点D是对应点.如果∠D=70°,∠CAB=50°,那么∠DAB度数是( )
如图,△ABC≌△BAD,点A和点B,点C和点D是对应点.如果∠D=70°,∠CAB=50°,那么∠DAB度数是( )
 如图,△ABC≌△BAD,点A和点B,点C和点D是对应点.如果∠D=70°,∠CAB=50°,那么∠DAB度数是( )
如图,△ABC≌△BAD,点A和点B,点C和点D是对应点.如果∠D=70°,∠CAB=50°,那么∠DAB度数是( )| A. | 80° | B. | 70° | C. | 60° | D. | 50° |
 如图,在?ABCD中,∠ADC的平分线交CB的延长线于点F,∠ABC的平分线交AD的延长线于点E,求证:四边形BFDE为平行四边形.
如图,在?ABCD中,∠ADC的平分线交CB的延长线于点F,∠ABC的平分线交AD的延长线于点E,求证:四边形BFDE为平行四边形.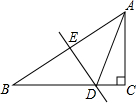 如图,△ABC中,∠C=90°,AB的垂直平分线交BC于D,如果∠B=35°,则∠CAD=20°.
如图,△ABC中,∠C=90°,AB的垂直平分线交BC于D,如果∠B=35°,则∠CAD=20°.